一、题目列表：

题目1、二叉树的深度
题目2、二叉搜索树的第k个节点
题目3、二叉树镜像
题目4、从上往下打印二叉树
题目5、二叉树中和为某一值的路径(一)
题目6、重建二叉树 JZ7
题目7、二叉树的下一个结点 JZ8
题目8、树的子结构 JZ26

定义：

1.二叉树遍历

二叉树的遍历分为两种方式：深度优先算法、广度优先算法(又叫层次遍历)

(1)深度优先算法

• 有三种方式：前序遍历、中序遍历、后序遍历
• 有两种算法可以实现三种遍历：递归和迭代(非递归)
• 【备注】：二叉树的深度优先遍历的非递归的通用做法是采用栈

(2)广度优先算法

• 有两种算法可以实现遍历：递归和迭代(非递归)
• 广度优先遍历的非递归的通用做法是采用队列

二.实现代码

1.深度优先算法

• 有三种方式：前序遍历、中序遍历、后序遍历
• 有两种算法可以实现三种遍历：递归和迭代(非递归)

#先创建二叉树
#!/usr/bin/python
class node:
    def __init__(self, val):
        self.val = val
        self.left = None
        self.right = None
 
root = node(5)
root.left = node(7)
root.right = node(8)
root.left.left = node(3)
root.left.right = node(4)
root.left.right.left = node(9)

#递归实现-前序遍历：
def preoder(root):                                                      
    if root is None:                                                            
        return                                                                  
    else:                                                                                                                                  
        print (root.val)                                                     
        preoder(root.left)                          
        preoder(root.right) 
      
#递归实现-中序遍历：
def minoder(root):                                                      
    if root is None:                                                            
        return                                                                  
    else:                                                                                                                                                                                    
        minoder(root.left) 
        print (root.val)                          
        minoder(root.right)       

#递归实现-后序遍历：
def postoder(root):                                                      
    if root is None:                                                            
        return                                                                  
    else:                                                                                                                                                                                    
        postoder(root.left)                
        postoder(root.right) 
        print (root.val)  


#迭代实现-前序遍历：
stack = [root]
result = [] 
while stack:
    t = stack.pop()
    if type(t) is node:
        stack.extend([t.right,t.left,t.val]) #只改变顺序就能实现前中后序遍历
    else:
        if t:
            result.append(t)
print(result)

#迭代实现-中序遍历：
stack = [root]
result = [] 
while stack:
    t = stack.pop()
    if type(t) is node:
        stack.extend([t.right,t.val,t.left])
    else:
        if t:
            result.append(t)
print(result)

#迭代实现-后序遍历：
stack = [root]
result = [] 
while stack:
    t = stack.pop()
    if type(t) is node:
        stack.extend([t.val,t.right,t.left])
    else:
        if t:
            result.append(t)
print(result)

2、广度优先算法

第一种：
def breadth_trav(root):
    if root is None:
        return
    queue = [root]
    while queue:
        cur_node = queue.pop(0)
        print(cur_node.val)
        if cur_node.left:
            queue.append(cur_node.left)
        if cur_node.right:
            queue.append(cur_node.right)

第二种：稍微变形
def TreeDepth( pRoot):
    if not pRoot:
        return 0
    qu = [pRoot]
    while(qu):
        tmp = []
        for i in qu:
            print(i.val)
            if i.left:
                tmp.append(i.left)
            if i.right:
                tmp.append(i.right)
        qu = tmp

二、题目

题目1、二叉树的深度

1.整体思路

方法一、递归
时间复杂度：O(n)O(n)O(n)，其中nnn为二叉树的节点数，遍历整棵二叉树
空间复杂度：O(n)O(n)O(n)，最坏情况下，二叉树化为链表，递归栈深度最大为nnn
方法二、层次遍历
时间复杂度：O(n)O(n)O(n)，其中nnn为二叉树的节点数，遍历整棵二叉树
空间复杂度：O(n)O(n)O(n)，最坏情况下，二叉树化为链表，递归栈深度最大为nnn

2.代码

方法一：递归
class Solution:
    def TreeDepth(self , pRoot: TreeNode) -> int:
        # write code here
        if not pRoot:
            return 0
        return max(self.TreeDepth(pRoot.left),self.TreeDepth(pRoot.right)) +1


方法二：层次遍历

class Solution:
    def TreeDepth(self , pRoot: TreeNode) -> int:
        # write code here
        if not pRoot:
            return 0
        qu = [pRoot]
        num = 0
        while(qu):
            tmp = []
            for i in qu:
                if i.left:
                    tmp.append(i.left)
                if i.right:
                    tmp.append(i.right)
            qu = tmp
            num +=1
        return num

题目2、二叉搜索树的第k个节点

来源：剑指offer第54题

1.整体思路

主要考点为：中序遍历
方法一、递归

2.代码

方法二：递归1
class Solution:
    def __init__(self):
        self.nodelist = []
    def result(self,root):
        if not root:
            return []
        self.result(root.left)
        self.nodelist.append(root.val)
        self.result(root.right)
        
    def KthNode(self , proot: TreeNode, k: int) -> int:
        # write code here
        self.result(proot)
        if not proot or k>len(self.nodelist) or k<=0:
            return -1
        return self.nodelist[k-1]


方法一：递归2
class Solution:
    def result(self,root):
        return self.result(root.left) + [root.val]+ self.result(root.right) if root else []
      
    def KthNode(self , proot: TreeNode, k: int) -> int:
        # write code here
        re = self.result(proot)
        if not proot or k>len(re) or k<=0:
            return -1
        return re[k-1]

题目3、二叉树镜像

来源：剑指offer第27题
操作给定的二叉树，将其变换为源二叉树的镜像。
原二叉树：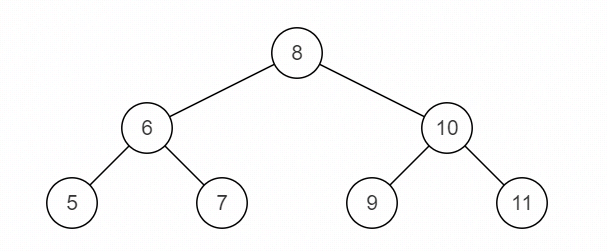

镜像：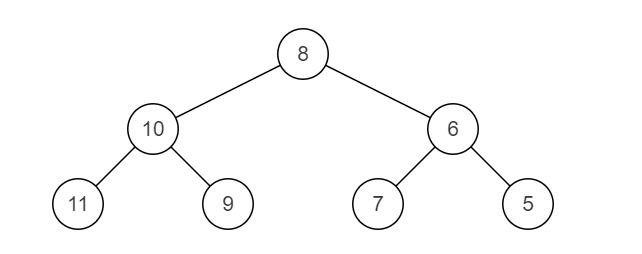

1.整体思路

主要考点为：层序遍历，
层序遍历每一层，让后让左右子节点换位置

2.代码

class Solution:
    def Mirror(self , pRoot: TreeNode) -> TreeNode:
        # write code here
        if not pRoot:
            return None
        qu = [pRoot]
        while(qu):
            node = qu.pop(0)
            if node.left:
                qu.append(node.left)
            if node.right:
                qu.append(node.right)
            tmp = node.left
            node.left = node.right
            node.right = tmp
        return pRoot

题目4、从上往下打印二叉树

来源：剑指offer第32题

1.整体思路

主要考点为：层序遍历

2.代码

class Solution:
    def PrintFromTopToBottom(self , pRoot: TreeNode) -> List[int]:
        # write code here
        if not pRoot:
            return None
        result = []
        qu = [pRoot]
        while(qu):
            node = qu.pop(0)
            result.append(node.val)
            if node.left:
                qu.append(node.left)
            if node.right:
                qu.append(node.right)
        return result

题目5、二叉树中和为某一值的路径(一)

来源：剑指offer第82题
描述：
给定一个二叉树root和一个值 sum ，判断是否有从根节点到叶子节点的节点值之和等于 sum 的路径。
1.该题路径定义为从树的根结点开始往下一直到叶子结点所经过的结点
2.叶子节点是指没有子节点的节点
3.路径只能从父节点到子节点，不能从子节点到父节点
4.总节点数目为n

1.整体思路

主要考点为：层序遍历

2.代码

class Solution:
    def hasPathSum(self , root: TreeNode, sum: int) -> bool:
        # write code here
        if not root:
            return False
        qu = [root]
        while qu:
            node = qu.pop()
            if not node.left and not node.right and node.val ==sum:
                return True
            if node.left:
                node.left.val = node.left.val + node.val
                qu.append(node.left)
            if node.right:
                node.right.val = node.right.val + node.val
                qu.append(node.right)   
        return False

题目6、重建二叉树 JZ7

来源：剑指offer第7题
描述：
给定节点数为 n 的二叉树的前序遍历和中序遍历结果，请重建出该二叉树并返回它的头结点。
例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6}，则重建出如下图所示。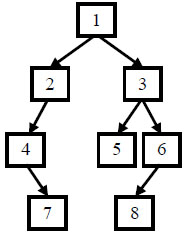

1.整体思路

1.先找根节点位置，根据根节点位置可以把前序遍历序列和和中序遍历序列分出来左树和右树
2.分别递归重建左树和右树

2.代码

# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None
#
# 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
#
# 
# @param pre int整型一维数组 
# @param vin int整型一维数组 
# @return TreeNode类
#
class Solution:
    def reConstructBinaryTree(self , pre: List[int], vin: List[int]) -> TreeNode:
        # write code here
        if not pre:
            return None
        root = TreeNode(pre[0])
        mind = vin.index(root.val) #找到根节点的位置，
        root.left = self.reConstructBinaryTree(pre[1:mind+1],vin[:mind])
        root.right = self.reConstructBinaryTree(pre[mind+1:],vin[mind+1:])
        return root

题目7、二叉树的下一个节点

来源：剑指offer第8题
描述：
给定一个二叉树其中的一个结点，请找出中序遍历顺序的下一个结点并且返回。注意，树中的结点不仅包含左右子结点，同时包含指向父结点的next指针。下图为一棵有9个节点的二叉树。树中从父节点指向子节点的指针用实线表示，从子节点指向父节点的用虚线表示

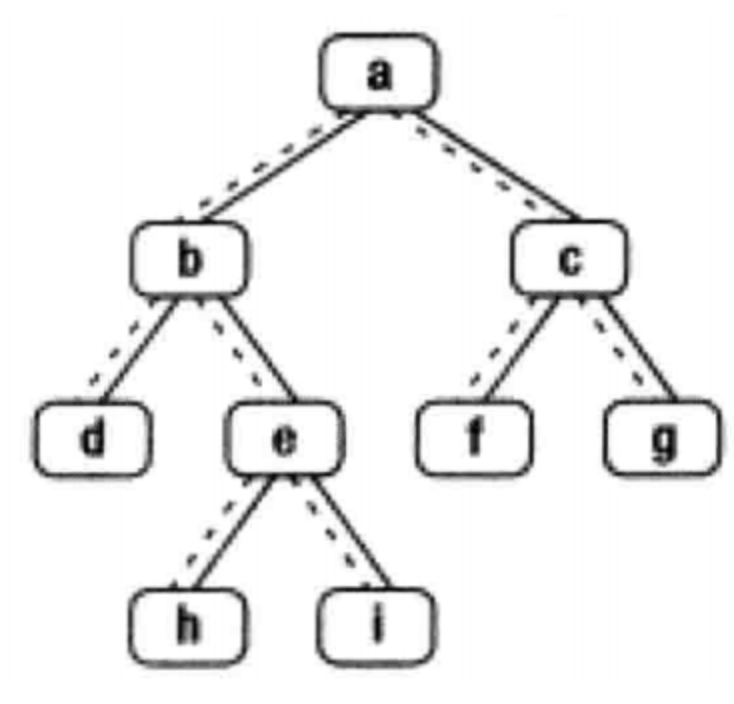
1.整体思路

2.代码

# -*- coding:utf-8 -*-
# class TreeLinkNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None
#         self.next = None
class Solution:
    def __init__(self):
        self.flag = None
        self.result = None
        self.nodes = []
    def GetNext(self, pNode):
        # 设置根节点占位符
        root = pNode
        self.flag = pNode
        #先找到根节点
        while root.next:
            root = root.next
        # 中序遍历
        self.InOrder(root)
        # 返回最终结果
        return self.result
            
    # 中序遍历
    def InOrder(self, root):
        if root == None:
            return
        self.InOrder(root.left)
        if self.nodes and self.nodes[-1] ==self.flag:
            self.result = root
        self.nodes.append(root)
        self.InOrder(root.right)     

题目8、树的子结构 JZ26
来源：剑指offer第26题
描述：
输入两棵二叉树A，B，判断B是不是A的子结构。（我们约定空树不是任意一个树的子结构）
假如给定A为{8,8,7,9,2,#,#,#,#,4,7}，B为{8,9,2}，2个树的结构如下，可以看出B是A的子结构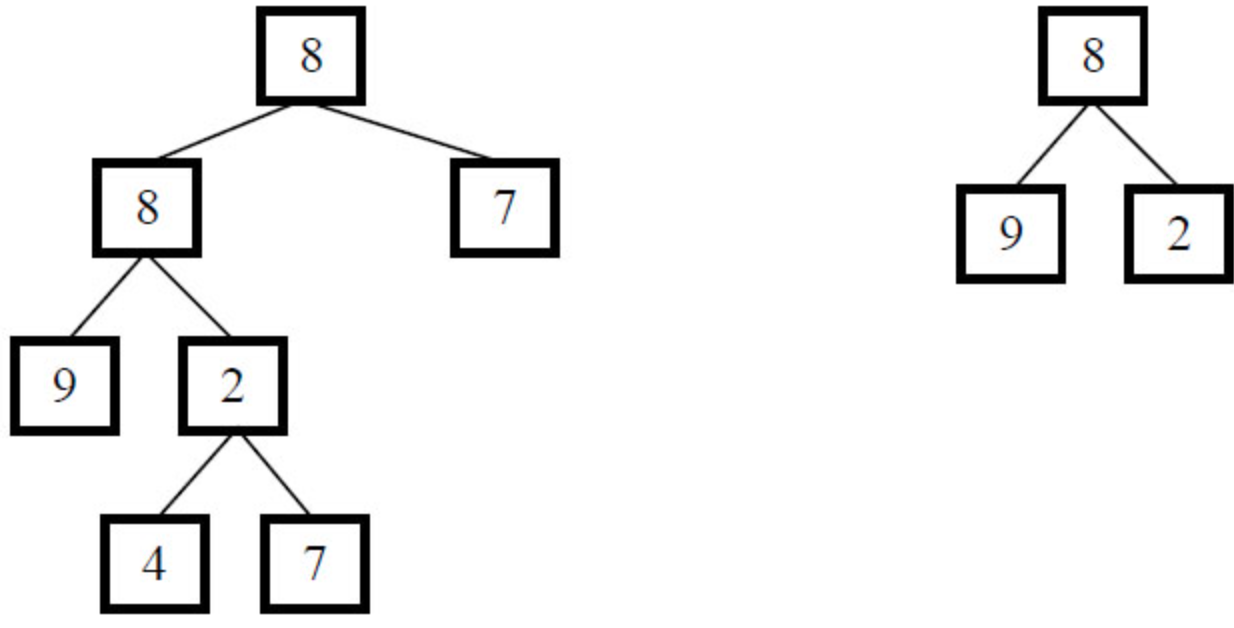

1.整体思路

2.代码

# -*- coding:utf-8 -*-
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None
class Solution:
    def HasSubtree(self, pRoot1, pRoot2):
        # write code here
        if pRoot1 == None:
            return False
        if pRoot2 == None:
            return False
        if self.is_subtree(pRoot1,pRoot2):
            return True
        if self.HasSubtree(pRoot1.left,pRoot2):
            return True
        if self.HasSubtree(pRoot1.right,pRoot2):
            return True
        
    def is_subtree(self,A,B):
        if B == None:
            return True
        if A == None:
            return False
        if A.val == B.val:
            return self.is_subtree(A.left,B.left) and self.is_subtree(A.right, B.right)
        else:
            return False
    

一、题目列表

题目1、构建乘积数组

题目2、调整数组顺序使奇数位于偶数前面(一)

题目3、把数组排成最小的数 JZ45

题目4、丑数 JZ49

题目5、数组中重复的数字 JZ3

题目6、旋转数组的最小数字 JZ11

题目7、打印从1到最大的n位数JZ17

题目8、两数之和 leetcode1 :给定一个整数数组 nums 和一个整数目标值 target

- 阅读剩余部分 -

一、题目列表

- 阅读剩余部分 -

分类方式

一.交换排序：1.冒泡排序，2.快速排序
二.插入排序：3.直接插入排序，4.希尔排序
三.选择排序：5.简单选择排序，6.堆排序
四.7.归并排序
五.8.基数排序

python实现

一、冒泡排序

思路：
两层循环：
第一层代表最右边最大数的位置。
第二层用来对比交换找出剩下的最大数

def sort(arr):
    l = len(arr)
    # 遍历所有数组元素
    for i in range(l):
        for j in range(0, l-i-1):
            if arr[j] > arr[j+1] :
                arr[j], arr[j+1] = arr[j+1], arr[j]
arr = [64, 34, 25, 12, 22, 11, 90]
sort(arr)
print (arr)

二、快速排序

1.递归排序算法

思路：

2.非递归排序算法

思路：和递归比较像，用栈来存划分区间，
在先找一个锚点，一最右边为例，通过锚点来划分子区间
参考：https://zhuanlan.zhihu.com/p/60756341

# -*- coding: UTF-8 -*-
# 递归排序算法
def sort(b):
    """快速排序"""
    if len(b) < 2:
        return b
    # 选取基准，随便选哪个都可以，选中间的便于理解
    mid = b[len(b)// 2]
    # 定义基准值左右两个数列
    left, right = [], []
    # 从原始数组中移除基准值
    b.remove(mid)
    for item in b:
        # 大于基准值放右边
        if item >= mid:
            right.append(item)
        else:
            # 小于基准值放左边
            left.append(item)
    # 使用迭代进行比较
    return sort(left) + [mid] + sort(right)

#非递归排序算法
def quicksortUnRecur( nums, beg, end):
        if beg >= end:
            return nums
        stack = [beg, end]
        while stack:
            beg, end = stack.pop(0), stack.pop(0)
            if beg >= end:
                continue
            i, pivot = beg-1, nums[end]
            for j in range(beg, end+1):
                if nums[j] <= pivot:
                    i += 1
                    nums[i], nums[j] = nums[j], nums[i]
            stack.extend([beg, i-1, i+1, end])

b = [11, 99, 33, 69, 77, 88, 55, 11, 33, 36, 39, 66, 44, 22]
print sort(b)

三、直接插入排序

1.思路

它的工作原理是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。

2.两种写法

有两种写法但是本质是一样的：
(1)标准的：不交换

• 设置一层循环,可以从0，也可以从1，都一样
• 然后设一个变量key=arr[i]，key用来记录，不交换，让后加while

(2)参考冒泡排序：交换

• 设置一层循环,可以从0，也可以从1，都一样
• 在设置一层循环，注意使用倒叙range(i-1, -1, -1)，然后进行交换

(1)标准的：不交换

# -*- coding: UTF-8 -*-
def sort(arr): 
    l = len(arr)
    for i in range(1, l): 
        key = arr[i] 
        j = i-1
        while j >=0 and key < arr[j] : 
                arr[j+1] = arr[j] 
                j -= 1
        arr[j+1] = key 
arr = [12, 11, 13, 5, 6] 
sort(arr) 
print(arr)

(2)参考冒泡排序：交换

# -*- coding: UTF-8 -*-
def insert(arr):
    l = len(arr)
    for i in range(l):
        for j in range(i-1, -1, -1):
            if arr[j] > arr[j+1]:
                arr[j+1], arr[j] = arr[j], arr[j+1]
            else:
                break
arr = [9, 5, 6, 7, 8 ]
insert(arr)
print arr

四、希尔排序

1.思路

希尔排序，也称递减增量排序算法，是插入排序的一种更高效的改进版本。但希尔排序是非稳定排序算法

# -*- coding: UTF-8 -*-

def shellSort(arr):
    n = len(arr)
    gap = int(n / 2)
    while gap > 0:
        for i in range(gap, n):
            temp = arr[i]
            j = i
            while j >= gap and arr[j - gap] > temp:
                arr[j] = arr[j - gap]
                j -= gap
            arr[j] = temp
        gap = int(gap / 2)


arr = [12, 34, 54, 2, 3]
shellSort(arr)
print arr

五、简单选择排序

1.思路

选择排序（Selection sort）是一种简单直观的排序算法。它的工作原理如下。首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置，然后，再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。

# -*- coding: UTF-8 -*-
def selectsort(arr):
    l = len(arr)
    for i in range(l):
        min_idx = i
        for j in range(i + 1, l):
            if arr[min_idx] > arr[j]:
                min_idx = j
        arr[i], arr[min_idx] = arr[min_idx], arr[i]
        
arr = [64, 25, 12, 22, 11]
selectsort(arr)
print (arr)

六、堆排序

1.思路

# -*- coding: UTF-8 -*-
def heapify(arr, n, i): 
    largest = i  
    l = 2 * i + 1     # left = 2*i + 1 
    r = 2 * i + 2     # right = 2*i + 2 
  
    if l < n and arr[i] < arr[l]: 
        largest = l 
  
    if r < n and arr[largest] < arr[r]: 
        largest = r 
  
    if largest != i: 
        arr[i],arr[largest] = arr[largest],arr[i]  # 交换
  
        heapify(arr, n, largest) 
  
def heapSort(arr): 
    n = len(arr) 
  
    # Build a maxheap. 
    for i in range(n, -1, -1): 
        heapify(arr, n, i) 
  
    # 一个个交换元素
    for i in range(n-1, 0, -1): 
        arr[i], arr[0] = arr[0], arr[i]   # 交换
        heapify(arr, i, 0) 
  
arr = [ 12, 11, 13, 5, 6, 7] 
heapSort(arr)
print arr

七、归并排序

1.思路

归并排序采用分而治之的原理：
一、将一个序列从中间位置分成两个序列；
二、在将这两个子序列按照第一步继续二分下去；
三、直到所有子序列的长度都为1，也就是不可以再二分截止。这时候再两两合并成一个有序序列即可。

# -*- coding: UTF-8 -*-
def merge(a, b):
    c = []
    h = j = 0
    while j < len(a) and h < len(b):
        if a[j] < b[h]:
            c.append(a[j])
            j += 1
        else:
            c.append(b[h])
            h += 1

    if j == len(a):
        for i in b[h:]:
            c.append(i)
    else:
        for i in a[j:]:
            c.append(i)

    return c


def merge_sort(lists):
    if len(lists) <= 1:
        return lists
    middle = len(lists)/2
    left = merge_sort(lists[:middle])
    right = merge_sort(lists[middle:])
    return merge(left, right)


if __name__ == '__main__':
    a = [4, 7, 8, 3, 5, 9]
    print merge_sort(a)

八、基数排序

1.思路

# -*- coding: UTF-8 -*-

分类方法

一、二分查找
二、

一、二分查找

1.思路

要求必须是有序列表

2.两种写法

1.递归查找
2.非递归查找

1.递归查找

# -*- coding: UTF-8 -*-


def binary_search1(arr, left, right, num):

    if left > right: #递归结束条件
        return -1
    mid = (left + right) // 2
    if num < arr[mid]:
        right = mid -1
    elif num > arr[mid]:
        left = mid + 1
    else:
        return mid
    return binary_search(arr, left, right, num)
    #这里之所以会有return是因为必须要接收值，不然返回None
    #回溯到最后一层的时候，如果没有return，那么将会返回None

arr = [11, 32, 51, 21, 42, 9, 5, 6, 7, 8]
print(arr)
arr.sort()
print(arr)
res = binary_search1(arr, 0, len(arr)-1,9)
print(res)

2.非递归查找

# -*- coding: UTF-8 -*-


def binary_search(arr, num):
    left = 0
    right = len(lis) - 1
    while left <= right:   #循环条件
        mid = (left + right) // 2   #获取中间位置，数字的索引（序列前提是有序的）
        if num < arr[mid]:  #如果查询数字比中间数字小，那就去二分后的左边找，
            right = mid - 1   #来到左边后，需要将右变的边界换为mid-1
        elif num > arr[mid]:   #如果查询数字比中间数字大，那么去二分后的右边找
            left = mid + 1    #来到右边后，需要将左边的边界换为mid+1
        else:
            return mid  #如果查询数字刚好为中间值，返回该值得索引
    return -1  #如果循环结束，左边大于了右边，代表没有找到

arr = [11, 32, 51, 21, 42, 9, 5, 6, 7, 8]
print(arr)
lis.sort()
print(arr)
res = binary_search(arr, 9)
print res