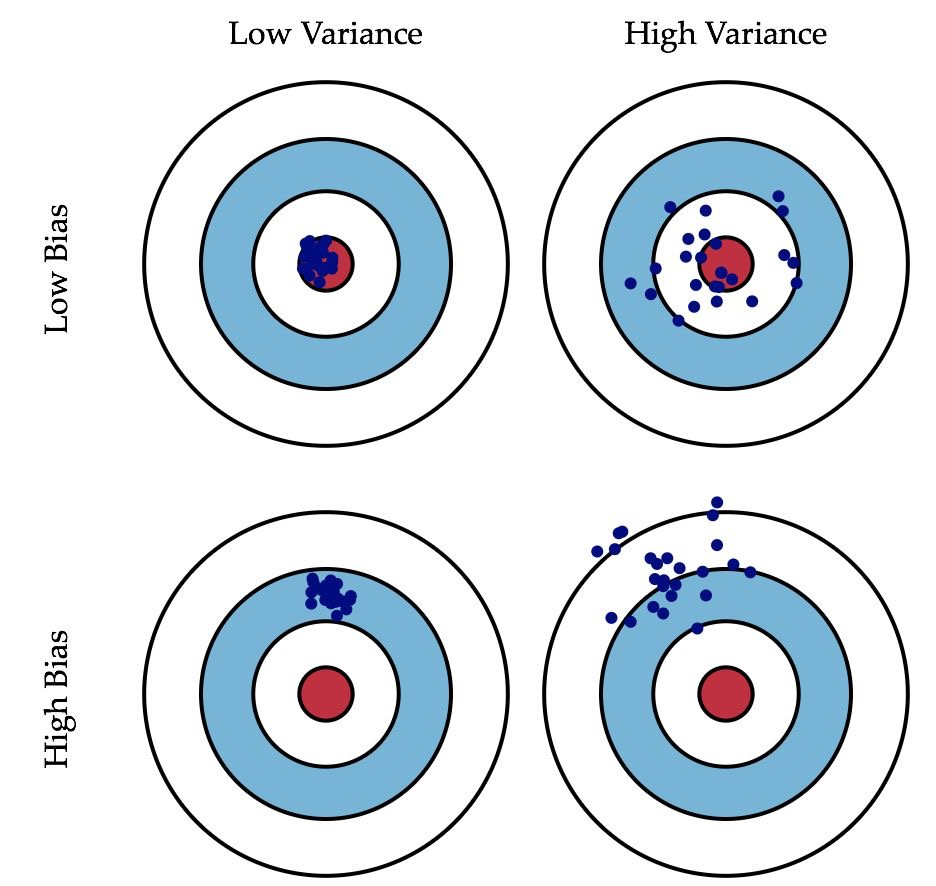
方差、偏差的定义
一、期望
也可以称为均值
假设每次的预测值为
$f(x1),f(x2),f(x3)...,f(x_n)$
每个预测值的概率分别为
$P(x1),P(x2),P(x3)....$
则期望为:
$\hat{f(x)}=p(x1)*f(x1) + p(x2)*f(x2) + p(x3)*f(x3) $
二、方差(与真实值无关)
度量了同样大小的训练集的变动所导致的学习性能的变化,即刻画了数据扰动造成的影响。
描述的是预测值的变化范围,离散程度,也就是离其期望值的距离。方差越大,数据的分布越分散,如下图右列所示。
---摘自《机器学习》,周志华
$var(x) = \frac{1}{n} \sum_{t=1}^{n}(f(x_{t})-\hat{f})^2$
三、偏差
度量学习算法的期望预测与真实结果的偏离程度,也叫拟合能力。
描述的是预测值(估计值)的期望与真实值之间的差距。偏差越大,越偏离真实数据,如下图第二行所示。
---摘自《机器学习》,周志华
$bias^2(x) = (\hat{f(x)}-y)^2$
y:真实值