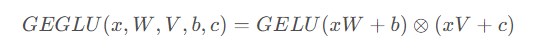常用激活函数
一、sigmoid 函数
1.公式
$y(x) = \frac{1}{1+e^{-x}}$
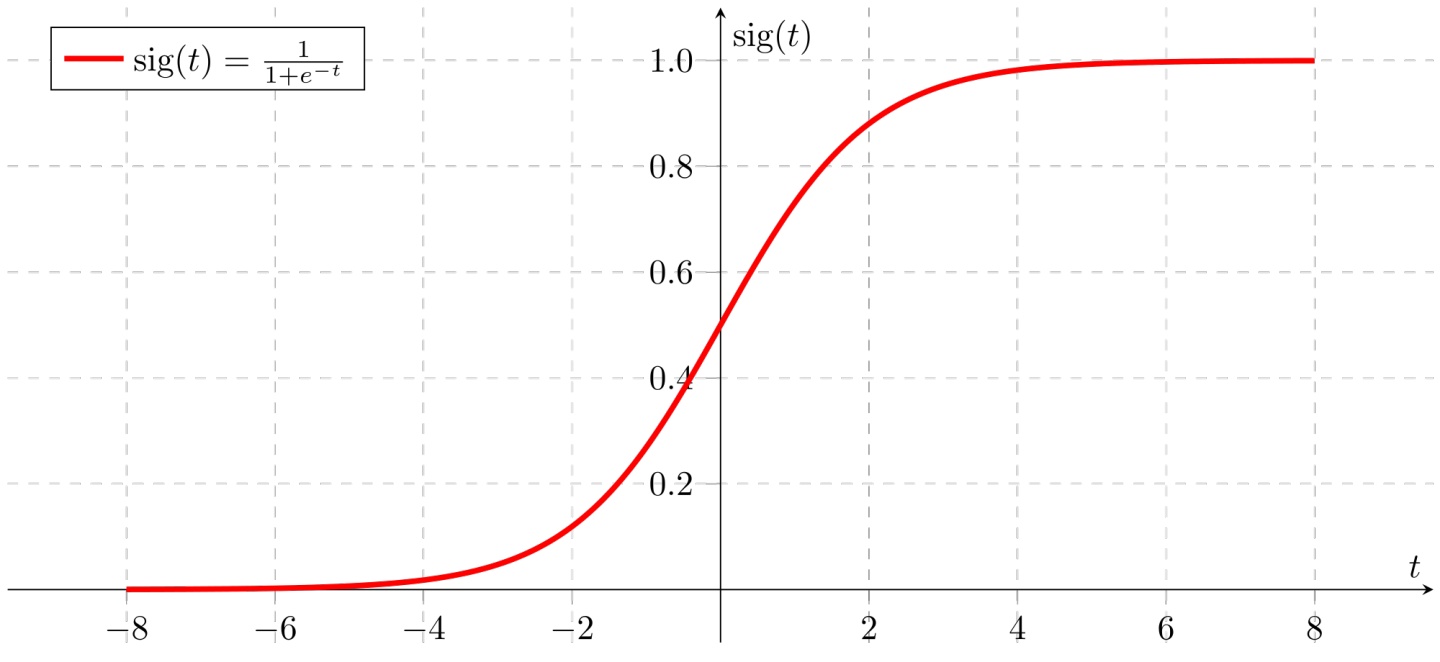
2.图像
3.性质
- (1)$y'= y*(1-y)$
- (2)$y'$导数的最大值为:1/4
4.作用
一般做神经网络最后一层的二分类来用
这个函数非常适合将输入分为两类。它的形状很缓和,因此它的梯度能得到很好的控制。
主要的缺点是,在极端情况下,函数输出变得非常平坦。这意味着它存在梯度消失的问题。
二、softmax函数
1.公式
$y(x)=\frac{e^xi}{\sum_{i=1}^m e^xi}$
2.图像
softmax没有图像,刻画的是百分比,解释图像为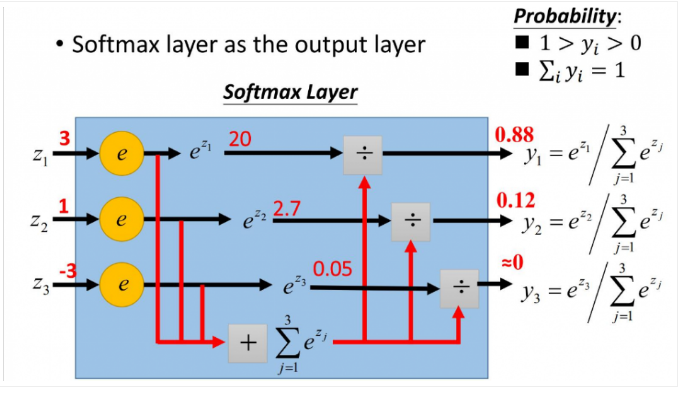
4.作用
一般做神经网络最后一层的多分类来用
三、tanh函数
1.定义
$y(x)=\frac{e^x - e^{-x}}{e^x + e^{-x}}$
2.图像
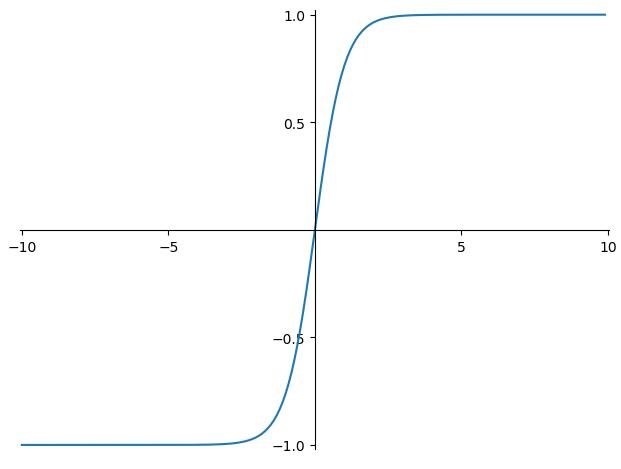
3.性质
- (1)$y'= 1- y^2$
- (2)$y'$导数的最大值为:1
4.作用
它与Sigmoid非常相似。函数曲线更陡峭,因此它的输出也将更强大。缺点与Sigmoid类似。
四、RELU函数
1.定义
线性整流函数(Linear rectification function),又称修正线性单元,是一种人工神经网络中常用的激活函数(activation function),通常指代以斜坡函数及其变种为代表的非线性函数。
公式: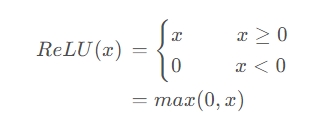
f(x)=max(0,x)
2.图像
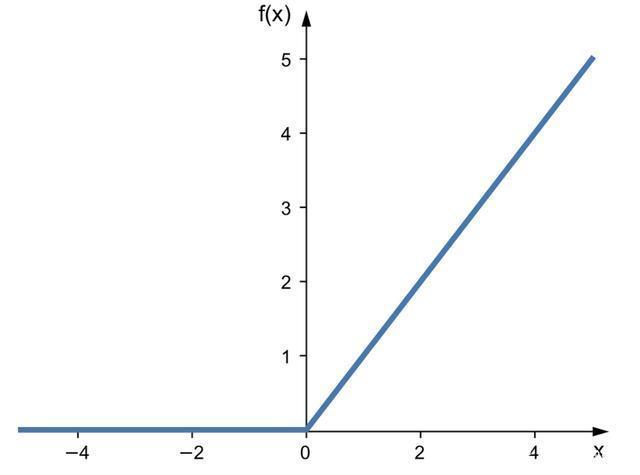
3.作用
它的输出范围从0到无穷大。这意味着它的输出可能会变得非常大,可能存在梯度爆炸问题。它还有个问题是左侧完全平坦,可能导致梯度消失。
ReLU计算简单,是神经网络内层最常用的激活函数。
参考文献
1.https://blog.csdn.net/u014665013/article/details/86600489
五、swish
1、定义
Swish是一个非线性激活函数,定义如下:
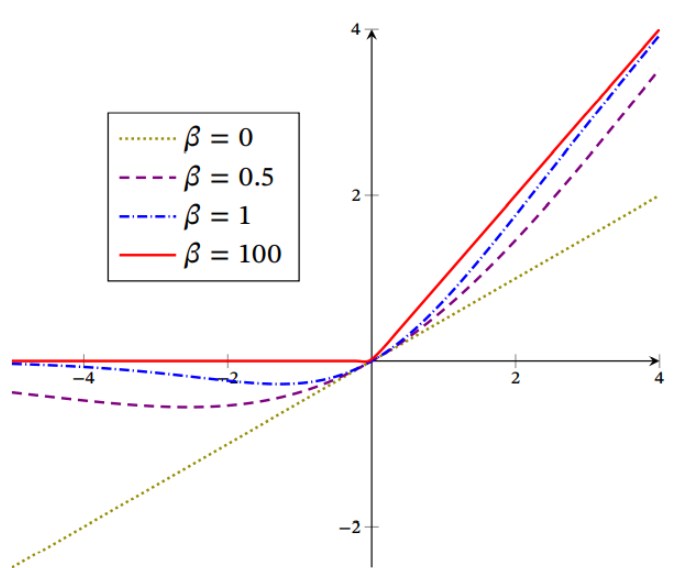
Swish(x) = x*sigmoid(ßx)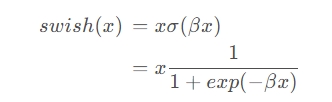
σ是sigmoid函数,β betaβ是可学习的参数或者一个固定超参数。
其中,ß 为可学习参数。Swish可以比ReLU激活函数更好,因为它在0附近提供了更平滑的转换,这可以带来更好的优化。
2、图像
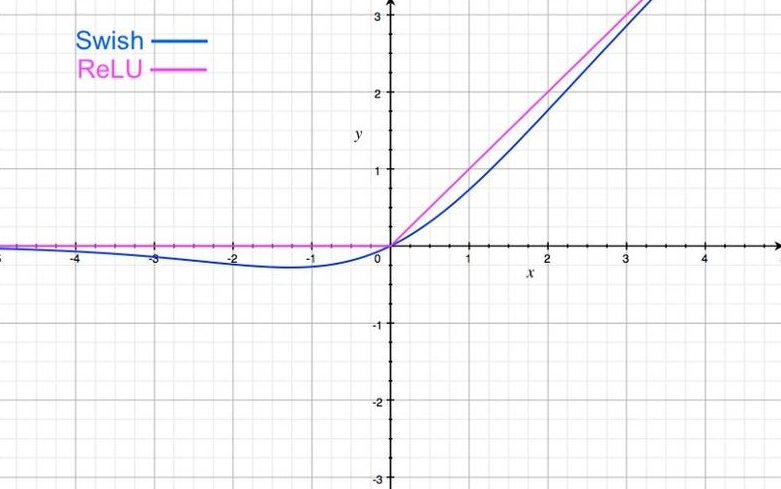
六、GLU系列
1、原生 GLU
(1).定义
GLU(x) = (Vx+c)⊗sigmoid(W1x+b)
⊗ :代表对应元素位分别相乘,是矩阵间的按元素乘。

2、GLU的各种变体
主要是将sigmoid换成 Relu、Gelu、swish等
(1) SwiGLU
SwiGLU可以看做采用Swish作为激活函数的GLU变体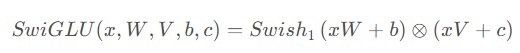
(2) ReGLU
ReGLU是采用ReLU函数作为激活函数的GLU变体
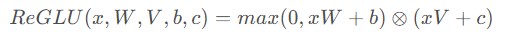
(3) GeGLU
GEGLU则可以看做采用GELU作为激活函数的GLU变体
GLM-130B 大模型使用的是GEGLU。