在深度学习中，向量、矩阵和张量是数学概念，它们用于表示和处理数据。下面是它们的定义：

一、向量（Vector）：

向量是一个一维数组，可以表示为一个有序的数值列表，通常用于表示单个数据点的特征。在数学上，向量可以是列向量（垂直于行向量）或行向量（水平于列向量）。在深度学习中，向量通常用来表示单个样本的特征。

• 向量是一组有序排列的数，可以是行向量或列向量。
• 行向量是一个水平排列的数值集合，通常表示为 $ \mathbf{v} = [v_1, v_2, \ldots, v_n]$
• 列向量是一个垂直排列的数值集合，通常表示为
  

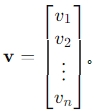
在深度学习中，向量通常用来表示一组特征或者是神经网络中的权重

二、矩阵（Matrix）：

矩阵是一个二维数组，由行和列组成。矩阵可以被看作是向量的集合，其中每个向量可以是列向量或行向量。在深度学习中，矩阵常用于表示多个数据点的特征集合，例如，一个矩阵的每一行可以代表一个样本，每一列代表一个特征。

• 矩阵是一个由数字按照矩形排列成的数组，有行和列的概念。
• 一个 m times nm×n 的矩阵可以表示为$ A = [a_{ij}] $，其中 $a_{ij} $ 表示位于第 ii 行第 jj 列的元素。
• 在深度学习中，矩阵常被用来表示权重参数、输入数据以及中间计算结果。

三、张量（Tensor）：

张量是向量和矩阵的推广。一个张量可以有任意数量的维度，而不仅仅是一维或二维。张量的阶数（order）或秩（rank）是指它的维度数。例如：

0阶张量是一个标量（scalar），是一个单一的数值。
1阶张量是一个向量。
2阶张量是一个矩阵。
3阶张量可以被看作是一个立方体，有三层维度。
4阶张量可以被看作是一个四维数组，等等。
在深度学习中，张量用于表示复杂的数据结构，如多维数组，这些数据结构可以包含图像、视频帧、序列数据等。张量运算（如加法、乘法等）是深度学习算法中的基础，它们允许我们执行复杂的数学操作来处理数据。