一、CRF模型的基本元素

1、 CRF的五个基本元素

HMM中，有5个基本元素：{I,O,A,B,π}，我结合序列标志任务对这5个基本元素做一个介绍：

(1)I:状态序列。在这里，是指每一个词语背后的标注。
(2)O:观测序列。在这里，是指每一个词语本身。
(3)A:转移特征函数(状态转移概率矩阵)：$m_kt_k(y_{i-1},y_i,x,i)$,k为特征个数
(4)B:状态特征函数(观测概率矩阵)：$u_ls_l(y_i,x,i)$,$l$为特征个数

2、CRF模型

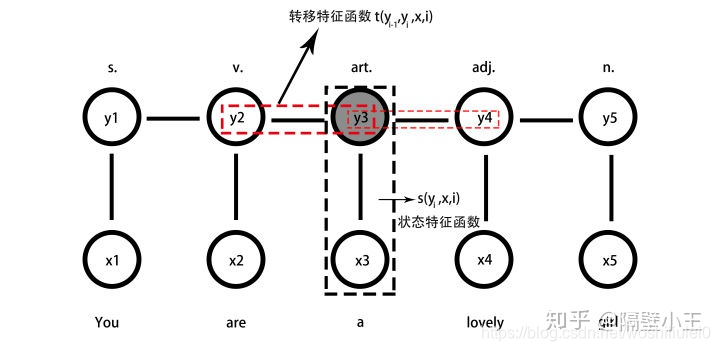
建模函数：
$P(y|x)=\frac{1}{Z(x)} exp(\sum λ_kt_k(y_{i-1},y_i,x,i)+\sum u_ls_l(y_i,x,i))$

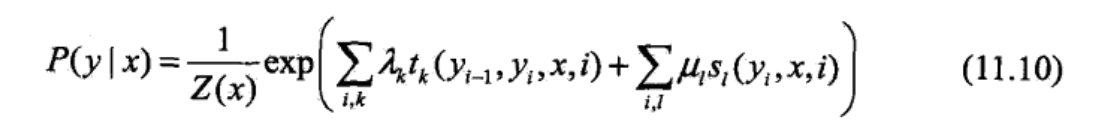
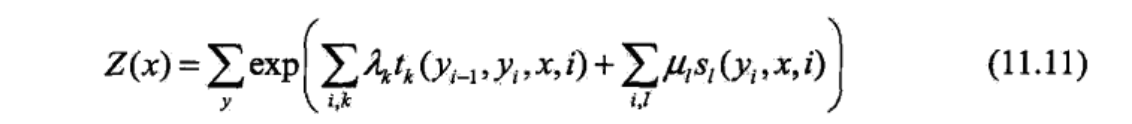
3、CRF模型的一个假设

假设：满足马尔科夫性：
$P(Y_i|X,Y_1,....,Y_{i-1},Y_{i+1},...y_n)=P(Y_i|X,Y_{i-1},Y_{i+1})$

二、CRF模型有三种应用场景

我们做命名实体识别只用到其中的一种——求观察序列的背后最可能的标注序列。CRF解决的三个问题：

1、Evaluation(概率计算问题)

已知模型参数 λ= (A, B, π),计算某个观测序列发生的概率，即求P(O|λ)

2、Learning(学习问题)

给定观测序列$O=(o_1,o_2,...,o_n)$，如何调整模型参数 λ=(π, A, B), 使得P(O|λ)最大？，这个就是求模型的算法

3、Decoding(预测问题或者叫解码问题) 最常用

给定观测序列O和模型 λ，求最有可能的状态序列S(s1,s2,...st+1)。
例如：通过实体标注和训练，我们可以得到模型λ，现在给定了一个观测序列=我在凤凰金融工作，求最有可能的命名实体有哪些，想找到对应的状态序列S=(我，在，凤凰金融，工作)。

三、模型由来

1.HMM假设缺点

• (1)齐次马尔科夫假设（又叫一阶马尔科夫假设）
  隐藏的马尔科夫链在任意时刻t的状态只依赖于前一时刻的状态，与其他时刻状态及观测状态无关。

$P(i_t|i_{t-1},o_{t-1},...,i_1) = P(i_t|i_{t-1})$

• (2)观测独立假设
  任意时刻的观测状态只依赖于该时刻的马尔科夫链的状态，与其他时刻的观测状态无关。

2.CRF优点

因为HMM有两个前提假设，所以HMM注定是局部最优解，无法达到全局最优解，也就无法达到最好的效果。

3.CRF算法

CRF解决了HMM两个假设的缺点，使用概率无向图，提出了两个特征函数
1.定义在边上的转移特征函数：$m_kt_k(y_{i-1},y_i,x,i)$
2.定义在节点上的状态特征函数：$u_ls_l(y_i,x,i)$
每个特征函数前面有系数
注意：

• 1.每个时刻t=i有多个特征函数，每个特征函数取值为1或者0，然后每个序列有多个时刻，所以模型上有两个加。
• 2.每个特征函数其实是个局部特征，可以对局部特征求和，将局部特征转化为全局特征。那么为啥求和是全局特征？其实求和的本意是求乘积，因为e为底的指数和就是乘积的形式，这就需要概率无向图求联合概率分布的算法。
• 3.CRF本质上是求概率无向图的联合概率分布，就是去各个时刻标注同时标注正确的联合概率，那么如何求概率无向图的联合概率分布呢？一般是将联合概率写成若干个子联合概率相乘的形式。也就是将联合概率因子分解。
• 4.联合概率因子分解：概率无向图的联合概率分布表示为其最大团上的随机变量函数的乘积，我们平时所说的CRF指的是线性连CRF，所以说每个时刻的i,o构成了一个最大团，所以证明了全局最优解就是局部最优解的和的形式。

参考：
1.https://spaces.ac.cn/archives/5542/comment-page-1
2.https://www.zhihu.com/question/35866596/answer/236886066
3.https://www.cnblogs.com/pinking/p/9194865.html

一、HMM模型的基本元素

1、 HMM的五个基本元素

HMM中，有5个基本元素：{I,O,A,B,π}，我结合序列标志任务对这5个基本元素做一个介绍：

(1)I:状态序列。在这里，是指每一个词语背后的标注。
(2)O:观测序列。在这里，是指每一个词语本身。
(3)A:状态转移概率矩阵。在这里，是指某一个标注转移到下一个标注的概率。
(4)B:观测概率矩阵，也就是发射概率矩阵。在这里，是指在某个标注下，生成某个词的概率。
(5)π:初始概率矩阵。在这里，是指每一个标注的初始化概率。
其中：
$I = ({i_1,i_2,i_3...i_N})$ 状态序列
$O = ({o_1,o_2,o_3...o_N})$ 观测序列
$A = [a_{ij}]_{N*N}$ 状态转移概率矩阵
$B = [b_j(k)]_{N*N}$ 观测概率矩阵
π 初始状态概率向量

HMM主要解决预测问题：也称为解码（decoding）问题。已知模型
λ＝(A，B, π) 和观测序列$O = ({o_1,o_2,o_3...o_N})$ ，，求对给定观测序列条件概率P(I|O)最大的状态序列 $I = ({i_1,i_2,i_3...i_N})$ 。即给定观测序列，求最有可能的对应的状态序列。

2、HMM模型

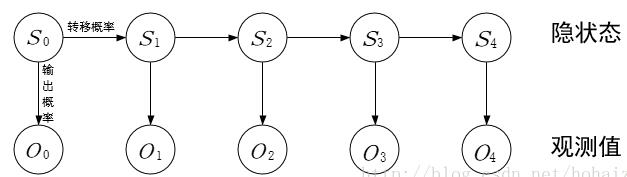
模型：λ = (A,B,π)
A,B,π为隐马尔可夫模型的三个要素
这三个元素都是通过统计得到的，这三个值就是模型的参数，得到这三个值的过程就是模型训练的过程，所以说HMM算法是比较简单的算法。模型已经知道了，可以认为各个状态的全连接路径已经知道了，给个观测序列，通过veterbi算法求解所有路径中的最优路径。

3、HMM模型的两个假设

• (1)齐次马尔科夫假设（又叫一阶马尔科夫假设）
  隐藏的马尔科夫链在任意时刻t的状态只依赖于前一时刻的状态，与其他时刻状态及观测状态无关。

$P(i_t|i_{t-1},o_{t-1},...,i_1) = P(i_t|i_{t-1})$

• (2)观测独立假设
  任意时刻的观测状态只依赖于该时刻的马尔科夫链的状态，与其他时刻的观测状态无关。

而以上的这些元素，都是可以从训练语料集中统计出来的。最后，我们根据这些统计值，应用维特比（viterbi）算法，就可以算出词语序列背后的标注序列了。

二、隐马尔可夫模型有三种应用场景

我们做命名实体识别只用到其中的一种——求观察序列的背后最可能的标注序列。
最后，来说下HMM解决的三个问题：

1、Evaluation(概率计算问题)

已知模型参数 λ= (A, B, π),计算某个观测序列发生的概率，即求P(O|λ)

2、Learning(学习问题)

给定观测序列$O=(o_1,o_2,...,o_n)$，如何调整模型参数 λ=(π, A, B), 使得P(O|λ)最大？，这个就是求模型的算法

3、Decoding(预测问题或者叫解码问题) 最常用

给定观测序列O和模型 λ，求最有可能的状态序列S(s1,s2,...st+1)。
例如：通过实体标注和训练，我们可以得到模型λ，现在给定了一个观测序列=我在凤凰金融工作，求最有可能的命名实体有哪些，想找到对应的状态序列S=(我，在，凤凰金融，工作)。

三、求模型λ：解决第二个问题

HMM是一种生成模型，所以求的是联合概率

注意：我们平时所说的，求模型指的是求目标函数，例如在线性回归中我们的目标函数为$h(λ)=λ_1X+λ_2$，求目标函数只需要求得参数λ，所以平时我们说求模型就是求参数。

$P(X,Y)$

四、维特比算法(Viterbi):解决第三个问题

维特比算法主要用动态规划来求解HMM的预测问题：一直模型和观测序列，求最可能的状态序列

假如状态序列为：$x_1,x_2,x_3 ... x_N$
对应观测序列为：$y_1,y_3,y_3 ... y_N$
那么我们的问题就转化为：在盲打时候已知输入序列$y_1,y_3,y_3 ... y_N$，对应的最可能汉字$x_1,x_2,x_3 ... x_N$。求最可能的汉字序列是什么？
公式：
$x_1,x_2,x_3 ... x_N = ArgMaxP(x_1,x_2,x_3 ... x_N|y_1,y_3,y_3 ... y_N)$
$= ArgMax \prod_{i=1}^N P(y_i|x_i)*P(x_i|x_{i-1})$

其中公式$ArgMax \prod_{i=1}^N P(y_i|x_i)*P(x_i|x_{i-1})$主要通过贝叶斯公式变换得来

我们知道贝叶斯公式为：$P(A|B) = \frac {P(B|A)*P(A)}{P(B)}$
那么$P(x|y) = \frac {P(y|x)*P(x)}{P(y)}$,其中P(y)为已知常数，其中P(x)实际为$P(x_t|x_{t-1})$,根据马尔科夫假设当前时刻假设之和前一时刻相关。

例如，输入观测序列：
我 爱 中 国
O O O B
O B O I
O O B I
B O I B
也就是求的第三行是最优路径：

四、维特比算法(Viterbi)

注意：viberbi算法计算过程中计算的是两个点之间的最短路径，不是计算的两个层之间的最短路径

1.性质

如果概率最大的路径p(或者说最短路径)经过某个点，比如途中的a，那么这条路径上的起始点S到a的这段子路径Q，一定是S到X22之间的最短路径。否则，用S到a的最短路径R替代Q，便构成一条比P更短的路径，这显然是矛盾的。证明了满足最优性原理。

2.算法

假如你从S和E之间找一条最短的路径，除了遍历完所有路径，还有什么更好的方法？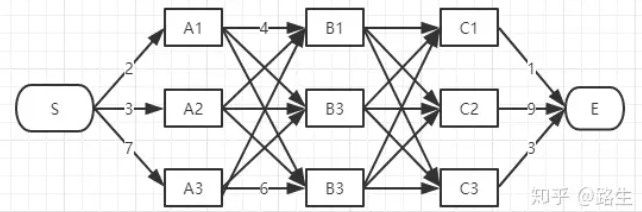

实际上在所有路径中肯定有一条最短路径：

我们开始从头一步一步求解：
(1)首先起点是S，从S到A列的路径有三种可能：S-A1、S-A2、S-A3，如下图：

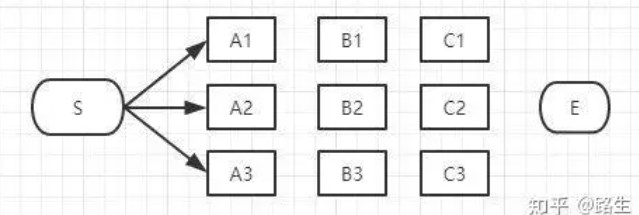
我们不能武断地说S-A1、S-A2、S-A3中的哪一段必定是全局最短路径中的一部分，目前为止任何一段都有可能是全局最短路径的备选项。
(2).然后开始第二层
<1>我们先从第二层的第一个节点开始：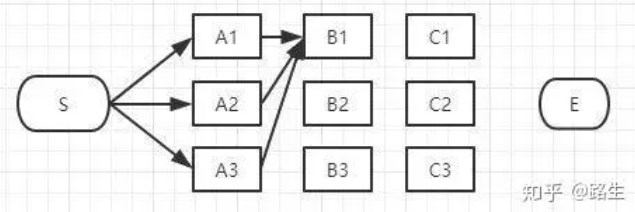

如上图，经过B1的所有路径只有3条：

S-A1-B1

S-A2-B1

S-A3-B1
如果说最终的第二层的节点是从B1经过的话，肯定要从这三条路径中选择一条最短的路径，那么其他的两条可以删除了。
<2>然后我们开始了第二层的第二个节点：

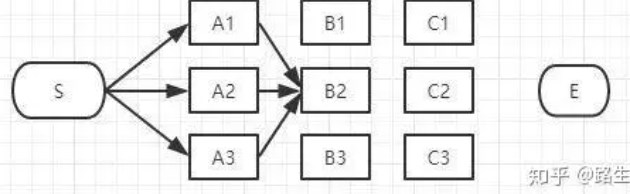
同理，如上图，经过B2的路径有3条：

S-A1-B2

S-A2-B2

S-A3-B2
如果说最终的第二层的节点是从B2经过的话，肯定要从这三条路径中选择一条最短的路径，那么其他的两条可以删除了。

<3>然后我们开始了第二层的第三个个节点：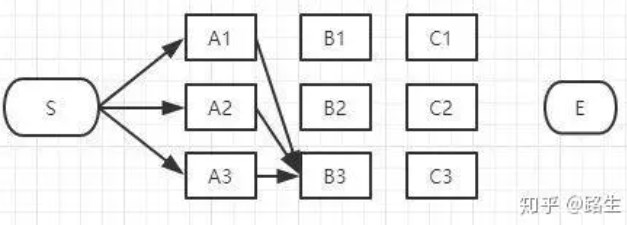

同理，如上图，经过B3的路径也有3条：

S-A1-B3

S-A2-B3

S-A3-B3
如果说最终的第二层的节点是从B3经过的话，肯定要从这三条路径中选择一条最短的路径，那么其他的两条可以删除了。
<4>所有第二层的阶段遍历完了之后，剩下三条路径了。

我们还没有足够的信息判断哪一条一定是全局最短路径的子路径。
(3)然后我们在第三层继续这个算法:
下来讲到C列了，类似上面说的B列，我们从C1、C2、C3一个个节点分析。
经过C1节点的路径有：

S-A3-B1-C1、

S-A1-B2-C1、

S-A2-B3-C1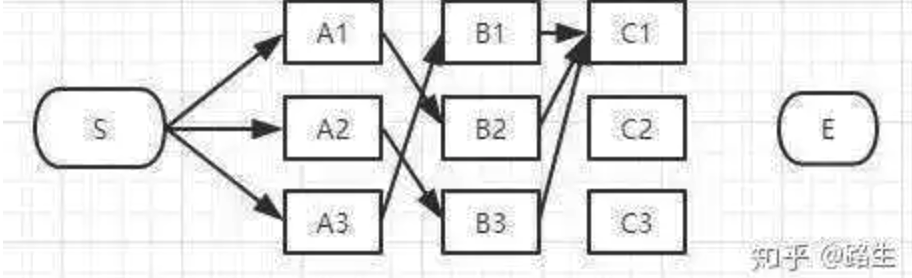

和B列的做法一样，从这三条路径中找到最短的那条（假定是S-A3-B1-C1），其它两条路径同样道理可以删掉了。那么经过C1的所有路径只剩一条，如下图：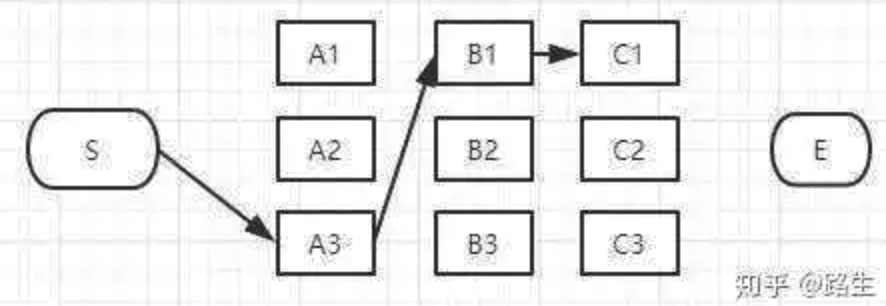

同理，我们可以找到经过C2和C3节点的最短路径，汇总一下：

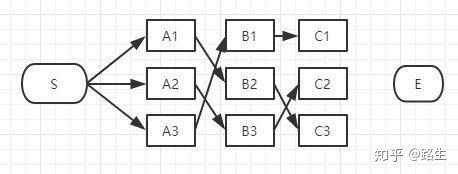
我们还没有足够的信息判断哪一条一定是全局最短路径的子路径。
(4)然后我们在最后一层继续这个算法: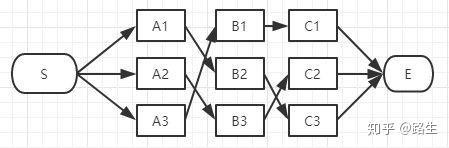

E点已经是终点了，我们稍微对比一下这三条路径的总长度就能知道哪条是最短路径了。

参考文章
https://clyyuanzi.gitbooks.io/julymlnotes/content/hmm.html
http://www.52nlp.cn/category/hidden-markov-model
https://www.lookfor404.com/%E7%94%A8%E9%9A%90%E9%A9%AC%E5%B0%94%E5%8F%AF%E5%A4%AB%E6%A8%A1%E5%9E%8Bhmm%E5%81%9A%E5%91%BD%E5%90%8D%E5%AE%9E%E4%BD%93%E8%AF%86%E5%88%AB-ner%E7%B3%BB%E5%88%97%E4%BA%8C/
https://www.zhihu.com/question/35866596/answer/236886066
http://www.hankcs.com/ml/conditional-random-field.html

https://www.zhihu.com/question/20136144/answer/763021768

对于CRF，直接用最大熵准则建模p(Y|X)的概率。
而HMM，是在做了markov假设下去建模p(Y,X)（即一切观察量的联合概率分布）

多模型评估的指标可以分为以下几个类别

一.Accuracy，Precision，Recall

要计算这几个指标先要了解几个概念：
FN：False Negative,被判定为负样本，但事实上是正样本。
FP：False Positive,被判定为正样本，但事实上是负样本。
TN：True Negative,被判定为负样本，事实上也是负样本。
TP：True Positive,被判定为正样本，事实上也是证样本。
1.Accuracy (准确率)
$ac=\frac {TP+TN}{TP+TN+FP+FN}$

2.Precision(精确率、查准率)
$P = \frac {TP}{TP+FP}$
解释：正样本占分类器所分的正样本的比例

3.Recall(召回率，查全率)
$R = \frac {TP}{TP + FN}$
解释：正样本占真正的正样本的比例

二、现实模型中的准招率

1.正样本的准确率，召回率

我们平常所说的准确率，召回率通常指正样本的，因为我们模板大多比较关心正样本。
$P = \frac {TP}{TP+FP}$
$R = \frac {TP}{TP + FN}$

2.负样本的准确率，召回率

$P = \frac {TN}{TN+FN}$
$R = \frac {TN}{TN + FP}$

3.整个样本的准确率，召回率

这里就要考虑宏平均和微平均

宏平均（Macro-averaging）

是先对每一个类统计指标值，然后在对所有类求算术平均值。

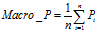
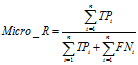
微平均（Micro-averaging）

是对数据集中的每一个实例不分类别进行统计建立全局混淆矩阵，然后计算相应指标。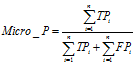

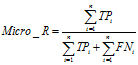
三、F1值

F1值是精确率和召回率的调和均值，即F1=2PR/(P+R)，相当于精确率和召回率的综合评价指标。

四、PR曲线

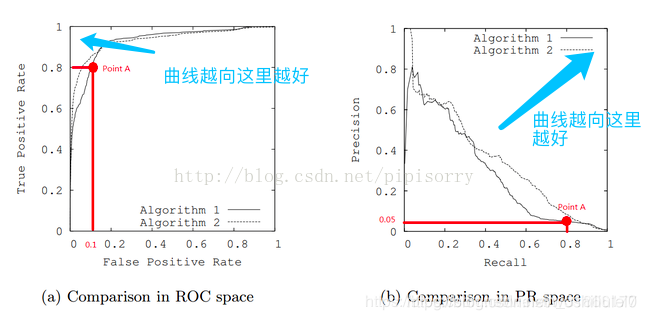
五、ROC曲线

1.定义

ROC全称是“受试者工作特征”(Receiver OperatingCharacteristic)曲线。我们根据学习器的预测结果，把阈值从0变到最大，即刚开始是把每个样本作为正例进行预测，随着阈值的增大，学习器预测正样例数越来越少，直到最后没有一个样本是正样例。在这一过程中，每次计算出两个重要量的值，分别以它们为横、纵坐标作图，就得到了“ROC曲线”。
###### 2.横纵坐标轴
纵坐标：真阳率：$TPR = \frac {TP}{TP + FN}$
横坐标：假阳率(误判率)：$FPR = \frac {TP}{TN + FP}$

3.为什么ROC曲线比PR曲线稳定

1.如果正负样本比例差不多，roc曲线和pr曲线基本一致。
2.如果样本比例失调，roc曲线比pr曲线更能判定模型好坏。
3.举个极端的例子：
100个去医院看病，其中99个艾滋病，一个正常人，结果医生将100个人都看成艾滋病人。则：
TP=99
FP=1
TN=0
FN=0
则：P=99%,R =100%,则PR曲线的效果就很好，实际分类效果不好
而：ROC曲线：TPR=100% ，FPR=100%，可看出ROC曲线效果不好，与实际一直。可以看出ROC曲线更好

六、AUC值

1.定义

那么这个指标代表什么呢？这个指标想表达的含义，简单来说其实就是随机抽出一对样本（一个正样本，一个负样本），然后用训练得到的分类器来对这两个样本进行预测，预测得到正样本的概率大于负样本概率的概率。

2.计算

• (1) 1. 最直观的
  根据AUC这个名称，我们知道，计算出ROC曲线下面的面积，就是AUC的值。事实上，这也是在早期 Machine Learning文献中常见的AUC计算方法。由于我们的测试样本是有限的。我们得到的AUC曲线必然是一个阶梯状的。因此，计算的AUC也就是这些阶梯 下面的面积之和。这样，我们先把score排序(假设score越大，此样本属于正类的概率越大)，然后一边扫描就可以得到我们想要的AUC。但是，这么 做有个缺点，就是当多个测试样本的score相等的时候，我们调整一下阈值，得到的不是曲线一个阶梯往上或者往右的延展，而是斜着向上形成一个梯形。此 时，我们就需要计算这个梯形的面积。由此，我们可以看到，用这种方法计算AUC实际上是比较麻烦的。
• (2)AUC的很有趣的性质
  它和Wilcoxon-Mann-Witney Test是等价的。而Wilcoxon-Mann-Witney Test就是测试任意给一个正类样本和一个负类样本，正类样本的score有多大的概率大于负类样本的score。

在有M个正样本,N个负样本的数据集里。一共有MN对样本（一对样本即，一个正样本与一个负样本）。统计这MN对样本里，正样本的预测概率大于负样本的预测概率的个数。

，其中，

这样说可能有点抽象，我举一个例子便能够明白。

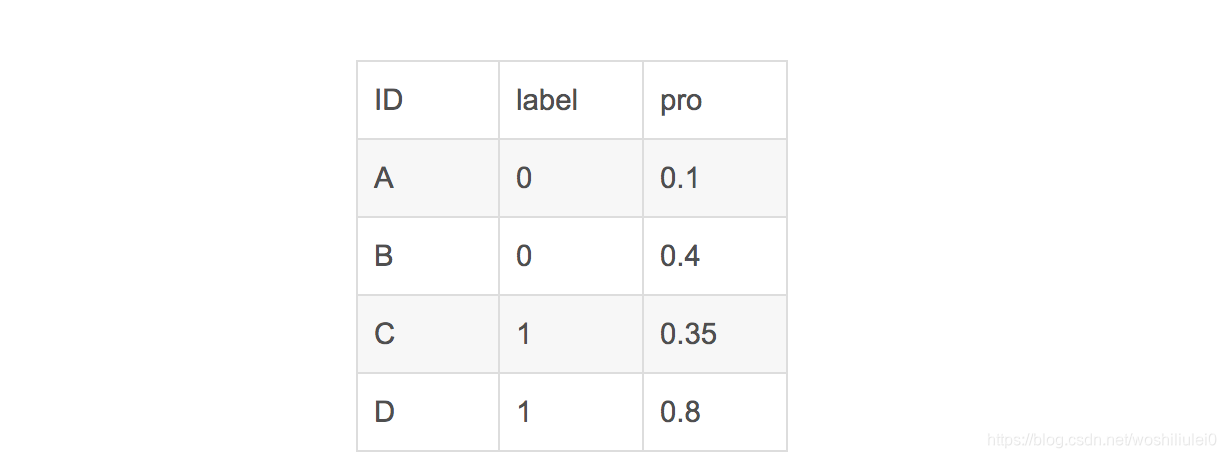
假设有4条样本。2个正样本，2个负样本，那么M*N=4。即总共有4个样本对。分别是：
（D,B）,（D,A）,(C,B),（C,A）。
在（D,B）样本对中，正样本D预测的概率大于负样本B预测的概率（也就是D的得分比B高），记为1
同理，对于（C,B）。正样本C预测的概率小于负样本C预测的概率，记为0.
最后可以算得，总共有3个符合正样本得分高于负样本得分，故最后的AUC为

在这个案例里，没有出现得分一致的情况，假如出现得分一致的时候，例如：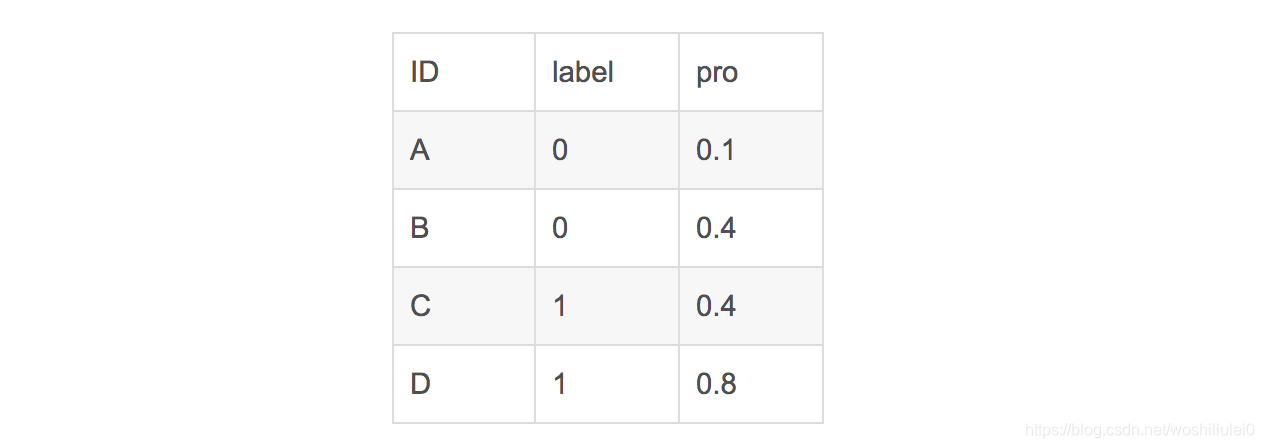

同样本是4个样本对，对于样本对（C,B）其I值为0.5。

最后的AUC为

一、背景

自从transformer出来之后，后面的算法基本上都是基于这个为基础，比如bert是以Encode层，GPT系列的GPT、GPT2、GPT3都是Decode层，下面我们主要讲解一下GPT-2。

1、论文

论文名字：《Language Models are Unsupervised Multitask Learners》
论文地址：Language Models are Unsupervised Multitask Learners

2、论文发表时间

时间：2019年2月
团队：openAI、特斯拉老板马斯克的公司

3、源码

源码：https://github.com/openai/gpt-2
官网：https://www.openai.com/blog/better-language-models/

二、架构

1、架构图

:注意：
GPT 使用 Transformer 的 Decoder 结构，并对 Transformer Decoder 进行了一些改动，原本的 Decoder 包含了两个 Multi-Head Attention 结构，GPT 只保留了 Mask Multi-Head Attention

2、网络结构参数

因为GPT-2在刚开始的时候openAI并没有开源，而是分了四个阶段放出来，每次放出来的预训练模型参数也不一样。
网络层数：24层
参数个数：15亿
参数文件大小：
训练数据大小：40G
最大上下文字数：1024

三、GPT-2相对于GPT的改进

GPT-2依然沿用GPT单向transformer的模式，只不过做了一些改进与改变。那GPT-2相对于GPT有哪些不同呢？看看下面几方面：

1. 增加数据集：

既然要博览群书，当然得先有书，所以GPT-2收集了更加广泛、数量更多的语料组成数据集。该数据集包含800万个网页，大小为40G。当然这些数据集是过滤后得到的高质量文本，这样效果才能更好的哦~

2. 增加网络参数：

GPT-2将Transformer堆叠的层数增加到48层，隐层的维度为1600，参数量更是达到了15亿。15亿什么概念呢，Bert的参数量也才只有3亿哦~当然，这样的参数量也不是说谁都能达到的，这也得取决于money的多少啊~

3. GPT-2去掉了fine-tuning层：

不再针对不同任务分别进行微调建模，而是不定义这个模型应该做什么任务，模型会自动识别出来需要做什么任务。这就好比一个人博览群书，你问他什么类型的问题，他都可以顺手拈来，GPT-2就是这样一个博览群书的模型。

4. 调整transformer：

将layer normalization放到每个sub-block之前，并在最后一个Self-attention后再增加一个layer normalization。

5. 其他：

GPT-2将词汇表数量增加到50257个；最大的上下文大小 (context size) 从GPT的512提升到了1024 tokens；batchsize增加到512。

6.Byte-level字节对编码

四、删除finue-tune直接做下游任务

1、Reading Comprehension：

使用 CoQA 数据集。输入是 document + conversation history + A: 来引导出答案。

2、Summarization：

用 TL;DR: 引导出摘要。

3、Translation：

为了引导模型做翻译，先找一个英法句子对 (en1, fr1)，然后想翻译英语句子 en 的时候，输入是 en1 = fr1 + en =，期待模型自己通过类比知道人类是想让他做翻译。结果模型真的悟出了一点儿道，fr-en 的翻译结果是 11.5 BLEU。这一结果是令人震惊的，因为模型在预训练的时候就没见过法语。用一个 byte-level language detector(https://github.com/CLD2Owners/cld2) 做更详细的分析发现，预训练的数据里混入了 10 MB 法语语料。考虑到语料的量级很少，这一结果依然是令人震惊的。

4、Natural Questions：

也是一个 QA 任务，为引导模型做问答，先搞一个 example qa pair (q1, a1)，然后给模型输入 q1 + a1 + q，模型就会回答出 q 的答案。