一、CRF模型的基本元素

1、 CRF的五个基本元素

HMM中，有5个基本元素：{I,O,A,B,π}，我结合序列标志任务对这5个基本元素做一个介绍：

(1)I:状态序列。在这里，是指每一个词语背后的标注。
(2)O:观测序列。在这里，是指每一个词语本身。
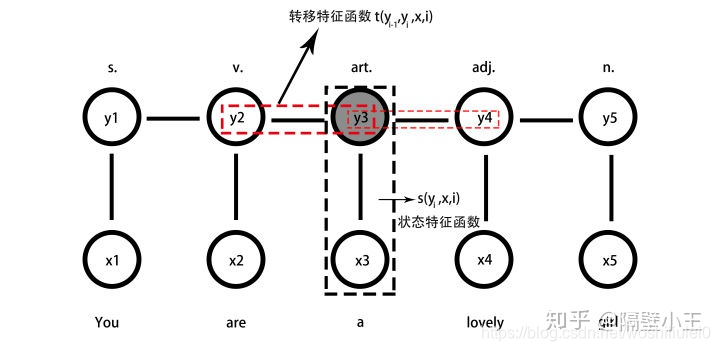
(3)A:转移特征函数(状态转移概率矩阵)：$m_kt_k(y_{i-1},y_i,x,i)$,k为特征个数
(4)B:状态特征函数(观测概率矩阵)：$u_ls_l(y_i,x,i)$,$l$为特征个数

2、CRF模型

20201010203039807.png

建模函数：
$P(y|x)=\frac{1}{Z(x)} exp(\sum λ_kt_k(y_{i-1},y_i,x,i)+\sum u_ls_l(y_i,x,i))$

20201009172828707.png

20201009172848167.png

20201009172913704.png

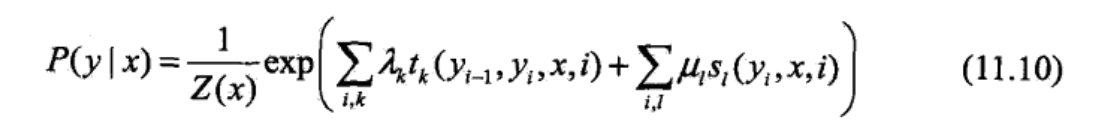
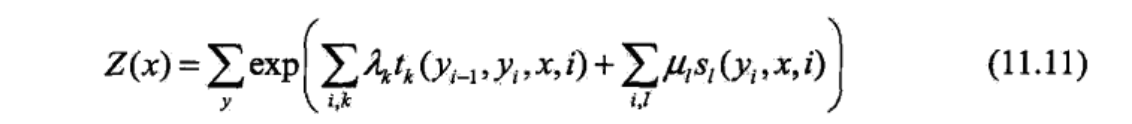
3、CRF模型的一个假设

假设：满足马尔科夫性：
$P(Y_i|X,Y_1,....,Y_{i-1},Y_{i+1},...y_n)=P(Y_i|X,Y_{i-1},Y_{i+1})$

二、CRF模型有三种应用场景

我们做命名实体识别只用到其中的一种——求观察序列的背后最可能的标注序列。CRF解决的三个问题：

1、Evaluation(概率计算问题)

已知模型参数 λ= (A, B, π),计算某个观测序列发生的概率，即求P(O|λ)

2、Learning(学习问题)

给定观测序列$O=(o_1,o_2,...,o_n)$，如何调整模型参数 λ=(π, A, B), 使得P(O|λ)最大？，这个就是求模型的算法

3、Decoding(预测问题或者叫解码问题) 最常用

给定观测序列O和模型 λ，求最有可能的状态序列S(s1,s2,...st+1)。
例如：通过实体标注和训练，我们可以得到模型λ，现在给定了一个观测序列=我在凤凰金融工作，求最有可能的命名实体有哪些，想找到对应的状态序列S=(我，在，凤凰金融，工作)。

三、模型由来

1.HMM假设缺点
  • (1)齐次马尔科夫假设（又叫一阶马尔科夫假设）
    隐藏的马尔科夫链在任意时刻t的状态只依赖于前一时刻的状态，与其他时刻状态及观测状态无关。

$P(i_t|i_{t-1},o_{t-1},...,i_1) = P(i_t|i_{t-1})$

  • (2)观测独立假设
    任意时刻的观测状态只依赖于该时刻的马尔科夫链的状态，与其他时刻的观测状态无关。
2.CRF优点

因为HMM有两个前提假设，所以HMM注定是局部最优解，无法达到全局最优解，也就无法达到最好的效果。

3.CRF算法

CRF解决了HMM两个假设的缺点，使用概率无向图，提出了两个特征函数
1.定义在边上的转移特征函数：$m_kt_k(y_{i-1},y_i,x,i)$
2.定义在节点上的状态特征函数：$u_ls_l(y_i,x,i)$
每个特征函数前面有系数
注意：

  • 1.每个时刻t=i有多个特征函数，每个特征函数取值为1或者0，然后每个序列有多个时刻，所以模型上有两个加。
  • 2.每个特征函数其实是个局部特征，可以对局部特征求和，将局部特征转化为全局特征。那么为啥求和是全局特征？其实求和的本意是求乘积，因为e为底的指数和就是乘积的形式，这就需要概率无向图求联合概率分布的算法。
  • 3.CRF本质上是求概率无向图的联合概率分布，就是去各个时刻标注同时标注正确的联合概率，那么如何求概率无向图的联合概率分布呢？一般是将联合概率写成若干个子联合概率相乘的形式。也就是将联合概率因子分解。
  • 4.联合概率因子分解：概率无向图的联合概率分布表示为其最大团上的随机变量函数的乘积，我们平时所说的CRF指的是线性连CRF，所以说每个时刻的i,o构成了一个最大团，所以证明了全局最优解就是局部最优解的和的形式。

参考：
1.https://spaces.ac.cn/archives/5542/comment-page-1
2.https://www.zhihu.com/question/35866596/answer/236886066
3.https://www.cnblogs.com/pinking/p/9194865.html

标签: none

添加新评论