模型评估的指标
多模型评估的指标可以分为以下几个类别
一.Accuracy,Precision,Recall
要计算这几个指标先要了解几个概念:
FN:False Negative,被判定为负样本,但事实上是正样本。
FP:False Positive,被判定为正样本,但事实上是负样本。
TN:True Negative,被判定为负样本,事实上也是负样本。
TP:True Positive,被判定为正样本,事实上也是证样本。
1.Accuracy (准确率)
$ac=\frac {TP+TN}{TP+TN+FP+FN}$
2.Precision(精确率、查准率)
$P = \frac {TP}{TP+FP}$
解释:正样本占分类器所分的正样本的比例
3.Recall(召回率,查全率)
$R = \frac {TP}{TP + FN}$
解释:正样本占真正的正样本的比例
二、现实模型中的准招率
1.正样本的准确率,召回率
我们平常所说的准确率,召回率通常指正样本的,因为我们模板大多比较关心正样本。
$P = \frac {TP}{TP+FP}$
$R = \frac {TP}{TP + FN}$
2.负样本的准确率,召回率
$P = \frac {TN}{TN+FN}$
$R = \frac {TN}{TN + FP}$
3.整个样本的准确率,召回率
这里就要考虑宏平均和微平均
宏平均(Macro-averaging)
是先对每一个类统计指标值,然后在对所有类求算术平均值。
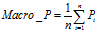
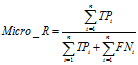
微平均(Micro-averaging)
是对数据集中的每一个实例不分类别进行统计建立全局混淆矩阵,然后计算相应指标。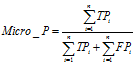
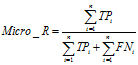
三、F1值
F1值是精确率和召回率的调和均值,即F1=2PR/(P+R),相当于精确率和召回率的综合评价指标。
四、PR曲线
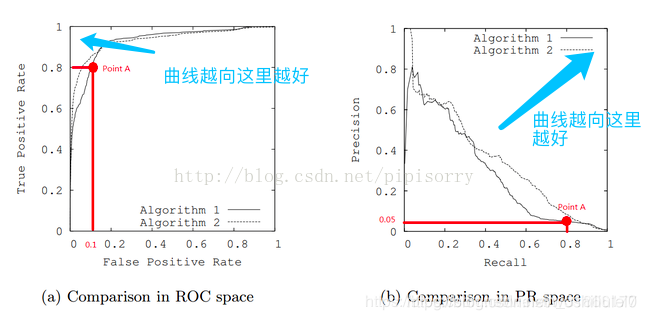
五、ROC曲线
1.定义
ROC全称是“受试者工作特征”(Receiver OperatingCharacteristic)曲线。我们根据学习器的预测结果,把阈值从0变到最大,即刚开始是把每个样本作为正例进行预测,随着阈值的增大,学习器预测正样例数越来越少,直到最后没有一个样本是正样例。在这一过程中,每次计算出两个重要量的值,分别以它们为横、纵坐标作图,就得到了“ROC曲线”。
###### 2.横纵坐标轴
纵坐标:真阳率:$TPR = \frac {TP}{TP + FN}$
横坐标:假阳率(误判率):$FPR = \frac {TP}{TN + FP}$

3.为什么ROC曲线比PR曲线稳定
1.如果正负样本比例差不多,roc曲线和pr曲线基本一致。
2.如果样本比例失调,roc曲线比pr曲线更能判定模型好坏。
3.举个极端的例子:
100个去医院看病,其中99个艾滋病,一个正常人,结果医生将100个人都看成艾滋病人。则:
TP=99
FP=1
TN=0
FN=0
则:P=99%,R =100%,则PR曲线的效果就很好,实际分类效果不好
而:ROC曲线:TPR=100% ,FPR=100%,可看出ROC曲线效果不好,与实际一直。可以看出ROC曲线更好
六、AUC值
1.定义
那么这个指标代表什么呢?这个指标想表达的含义,简单来说其实就是随机抽出一对样本(一个正样本,一个负样本),然后用训练得到的分类器来对这两个样本进行预测,预测得到正样本的概率大于负样本概率的概率。
2.计算
- (1) 1. 最直观的
根据AUC这个名称,我们知道,计算出ROC曲线下面的面积,就是AUC的值。事实上,这也是在早期 Machine Learning文献中常见的AUC计算方法。由于我们的测试样本是有限的。我们得到的AUC曲线必然是一个阶梯状的。因此,计算的AUC也就是这些阶梯 下面的面积之和。这样,我们先把score排序(假设score越大,此样本属于正类的概率越大),然后一边扫描就可以得到我们想要的AUC。但是,这么 做有个缺点,就是当多个测试样本的score相等的时候,我们调整一下阈值,得到的不是曲线一个阶梯往上或者往右的延展,而是斜着向上形成一个梯形。此 时,我们就需要计算这个梯形的面积。由此,我们可以看到,用这种方法计算AUC实际上是比较麻烦的。 - (2)AUC的很有趣的性质
它和Wilcoxon-Mann-Witney Test是等价的。而Wilcoxon-Mann-Witney Test就是测试任意给一个正类样本和一个负类样本,正类样本的score有多大的概率大于负类样本的score。
在有M个正样本,N个负样本的数据集里。一共有MN对样本(一对样本即,一个正样本与一个负样本)。统计这MN对样本里,正样本的预测概率大于负样本的预测概率的个数。
,其中, 
这样说可能有点抽象,我举一个例子便能够明白。
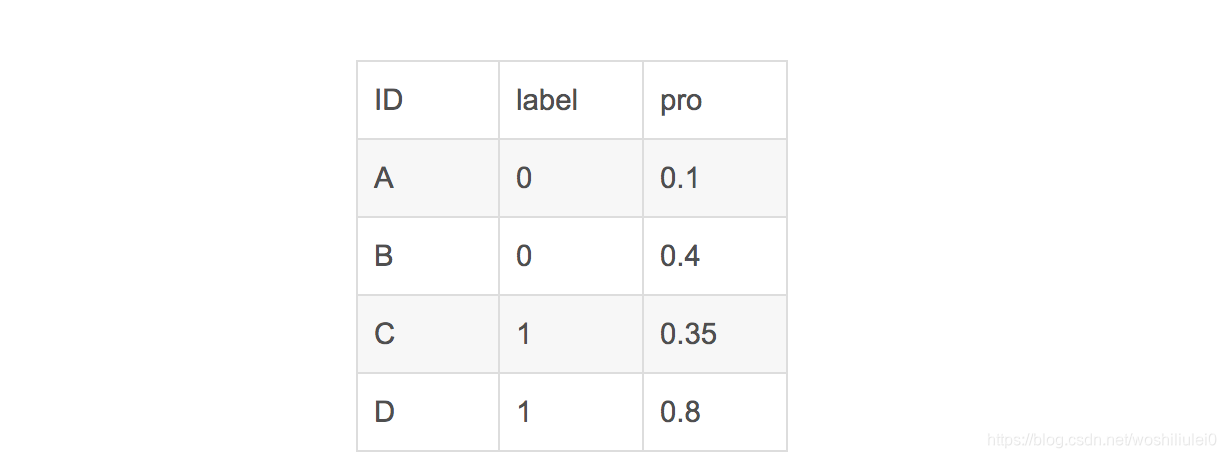
假设有4条样本。2个正样本,2个负样本,那么M*N=4。即总共有4个样本对。分别是:
(D,B),(D,A),(C,B),(C,A)。
在(D,B)样本对中,正样本D预测的概率大于负样本B预测的概率(也就是D的得分比B高),记为1
同理,对于(C,B)。正样本C预测的概率小于负样本C预测的概率,记为0.
最后可以算得,总共有3个符合正样本得分高于负样本得分,故最后的AUC为 
在这个案例里,没有出现得分一致的情况,假如出现得分一致的时候,例如: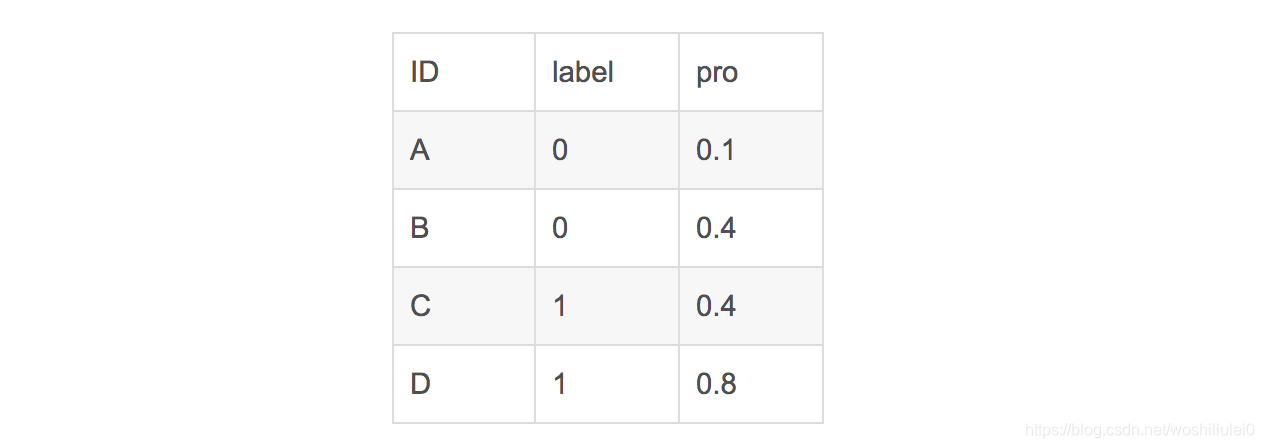
同样本是4个样本对,对于样本对(C,B)其I值为0.5。

最后的AUC为