各向异性
一、定义
各向异性(Anisotropic) 的概念在BERT-flow的文章中有明确的定义:
(1)“Anisotropic” means word embeddings occupy a narrow cone in the vector space.
翻译过来就是:“各向异性”表示词嵌入在向量空间中占据了一个狭窄的圆锥形体。但这个定义有点过于场景化,实际上各向异性的表现形式并不一定是锥形。
(2)各向异性:词向量是有维度的,每个维度上基向量单位向量长度不一样,就是各向异性的。这样就会造成我们计算向量相似度的时候产生偏差,如下图是举例:例如下图中,基向量是非正交,且各向异性(基向量单位向量长度不一样),计算向量x1与x2的cos相似度为0,x1与x3的cos相似度为0(正交),但是我们从几何角度上看,其实x1是与x3更相似的,所以导致计算相似度结果也会有问题。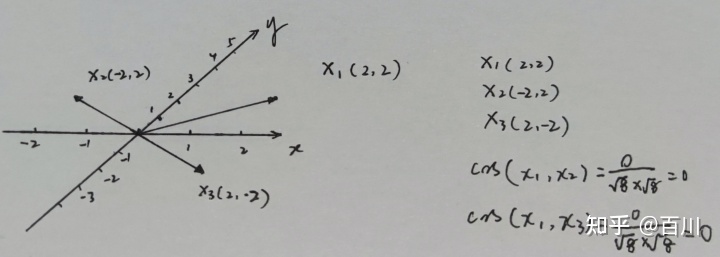
二、缺点
各向异性就有个问题,那就是最后学到的向量都挤在一起,彼此之间计算余弦相似度都很高,并不是一个很好的表示。一个好的向量表示应该同时满足Alignment 和 uniformity,前者表示相似的向量距离应该相近,后者就表示向量在空间上应该尽量均匀,最好是各向同性的。
三、解决办法
通过:BERT-flow、bert-whitening、SimCse、SBert
1. BERT-flow映射为各向同性
BERT-flow的工作就是将原来的分布校准为高斯分布。标准的高斯分布就是各向同性的。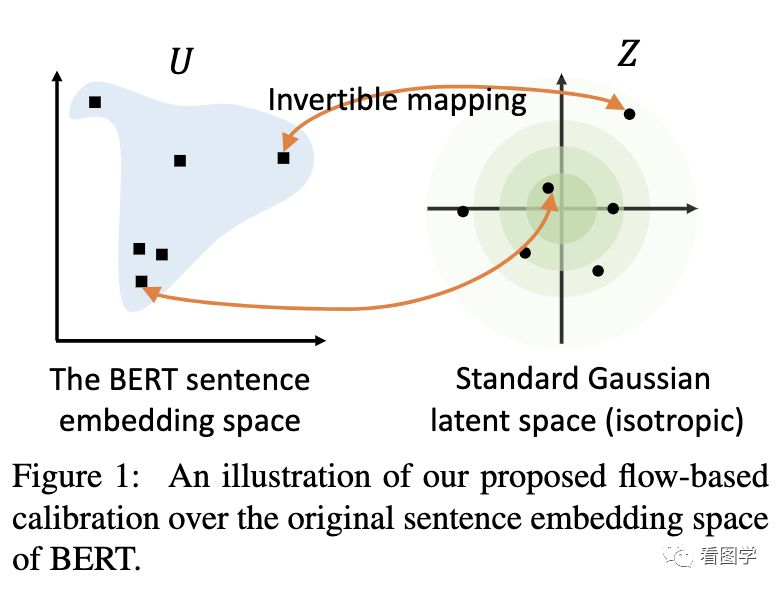
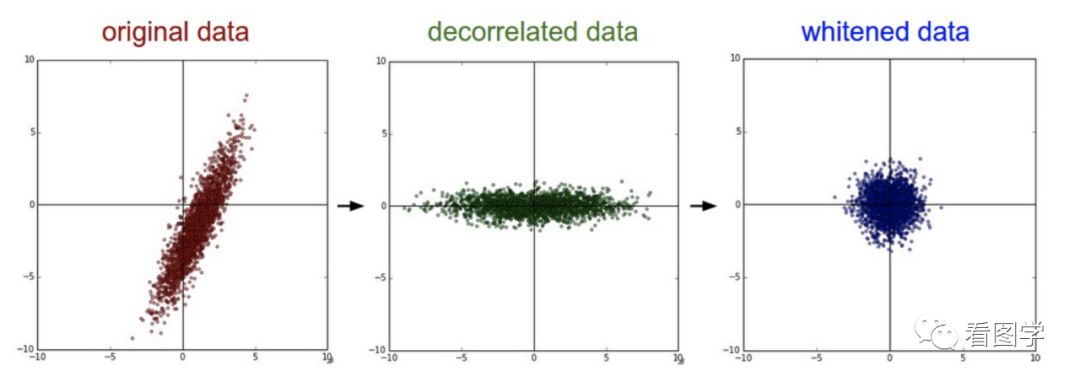
2. bert-whitening
类似的还有whitening操作。大概流程就是根据SVD分解的结果,旋转缩放后得到一个标准正态分布。