一、HMM模型的基本元素

1、 HMM的五个基本元素

HMM中，有5个基本元素：{I,O,A,B,π}，我结合序列标志任务对这5个基本元素做一个介绍：

(1)I:状态序列。在这里，是指每一个词语背后的标注。
(2)O:观测序列。在这里，是指每一个词语本身。
(3)A:状态转移概率矩阵。在这里，是指某一个标注转移到下一个标注的概率。
(4)B:观测概率矩阵，也就是发射概率矩阵。在这里，是指在某个标注下，生成某个词的概率。
(5)π:初始概率矩阵。在这里，是指每一个标注的初始化概率。
其中：
$I = ({i_1,i_2,i_3...i_N})$ 状态序列
$O = ({o_1,o_2,o_3...o_N})$ 观测序列
$A = [a_{ij}]_{N*N}$ 状态转移概率矩阵
$B = [b_j(k)]_{N*N}$ 观测概率矩阵
π 初始状态概率向量

HMM主要解决预测问题：也称为解码（decoding）问题。已知模型
λ＝(A，B, π) 和观测序列$O = ({o_1,o_2,o_3...o_N})$ ，，求对给定观测序列条件概率P(I|O)最大的状态序列 $I = ({i_1,i_2,i_3...i_N})$ 。即给定观测序列，求最有可能的对应的状态序列。

2、HMM模型

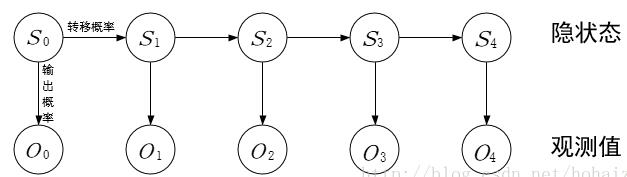
模型：λ = (A,B,π)
A,B,π为隐马尔可夫模型的三个要素
这三个元素都是通过统计得到的，这三个值就是模型的参数，得到这三个值的过程就是模型训练的过程，所以说HMM算法是比较简单的算法。模型已经知道了，可以认为各个状态的全连接路径已经知道了，给个观测序列，通过veterbi算法求解所有路径中的最优路径。

3、HMM模型的两个假设

• (1)齐次马尔科夫假设（又叫一阶马尔科夫假设）
  隐藏的马尔科夫链在任意时刻t的状态只依赖于前一时刻的状态，与其他时刻状态及观测状态无关。

$P(i_t|i_{t-1},o_{t-1},...,i_1) = P(i_t|i_{t-1})$

• (2)观测独立假设
  任意时刻的观测状态只依赖于该时刻的马尔科夫链的状态，与其他时刻的观测状态无关。

而以上的这些元素，都是可以从训练语料集中统计出来的。最后，我们根据这些统计值，应用维特比（viterbi）算法，就可以算出词语序列背后的标注序列了。

二、隐马尔可夫模型有三种应用场景

我们做命名实体识别只用到其中的一种——求观察序列的背后最可能的标注序列。
最后，来说下HMM解决的三个问题：

1、Evaluation(概率计算问题)

已知模型参数 λ= (A, B, π),计算某个观测序列发生的概率，即求P(O|λ)

2、Learning(学习问题)

给定观测序列$O=(o_1,o_2,...,o_n)$，如何调整模型参数 λ=(π, A, B), 使得P(O|λ)最大？，这个就是求模型的算法

3、Decoding(预测问题或者叫解码问题) 最常用

给定观测序列O和模型 λ，求最有可能的状态序列S(s1,s2,...st+1)。
例如：通过实体标注和训练，我们可以得到模型λ，现在给定了一个观测序列=我在凤凰金融工作，求最有可能的命名实体有哪些，想找到对应的状态序列S=(我，在，凤凰金融，工作)。

三、求模型λ：解决第二个问题

HMM是一种生成模型，所以求的是联合概率

注意：我们平时所说的，求模型指的是求目标函数，例如在线性回归中我们的目标函数为$h(λ)=λ_1X+λ_2$，求目标函数只需要求得参数λ，所以平时我们说求模型就是求参数。

$P(X,Y)$

四、维特比算法(Viterbi):解决第三个问题

维特比算法主要用动态规划来求解HMM的预测问题：一直模型和观测序列，求最可能的状态序列

假如状态序列为：$x_1,x_2,x_3 ... x_N$
对应观测序列为：$y_1,y_3,y_3 ... y_N$
那么我们的问题就转化为：在盲打时候已知输入序列$y_1,y_3,y_3 ... y_N$，对应的最可能汉字$x_1,x_2,x_3 ... x_N$。求最可能的汉字序列是什么？
公式：
$x_1,x_2,x_3 ... x_N = ArgMaxP(x_1,x_2,x_3 ... x_N|y_1,y_3,y_3 ... y_N)$
$= ArgMax \prod_{i=1}^N P(y_i|x_i)*P(x_i|x_{i-1})$

其中公式$ArgMax \prod_{i=1}^N P(y_i|x_i)*P(x_i|x_{i-1})$主要通过贝叶斯公式变换得来

我们知道贝叶斯公式为：$P(A|B) = \frac {P(B|A)*P(A)}{P(B)}$
那么$P(x|y) = \frac {P(y|x)*P(x)}{P(y)}$,其中P(y)为已知常数，其中P(x)实际为$P(x_t|x_{t-1})$,根据马尔科夫假设当前时刻假设之和前一时刻相关。

例如，输入观测序列：
我 爱 中 国
O O O B
O B O I
O O B I
B O I B
也就是求的第三行是最优路径：

四、维特比算法(Viterbi)

注意：viberbi算法计算过程中计算的是两个点之间的最短路径，不是计算的两个层之间的最短路径

1.性质

如果概率最大的路径p(或者说最短路径)经过某个点，比如途中的a，那么这条路径上的起始点S到a的这段子路径Q，一定是S到X22之间的最短路径。否则，用S到a的最短路径R替代Q，便构成一条比P更短的路径，这显然是矛盾的。证明了满足最优性原理。

2.算法

假如你从S和E之间找一条最短的路径，除了遍历完所有路径，还有什么更好的方法？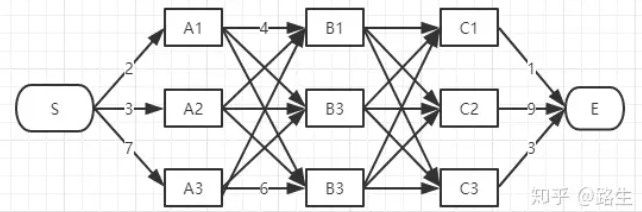

实际上在所有路径中肯定有一条最短路径：

我们开始从头一步一步求解：
(1)首先起点是S，从S到A列的路径有三种可能：S-A1、S-A2、S-A3，如下图：

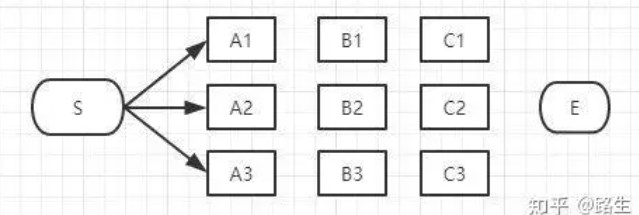
我们不能武断地说S-A1、S-A2、S-A3中的哪一段必定是全局最短路径中的一部分，目前为止任何一段都有可能是全局最短路径的备选项。
(2).然后开始第二层
<1>我们先从第二层的第一个节点开始：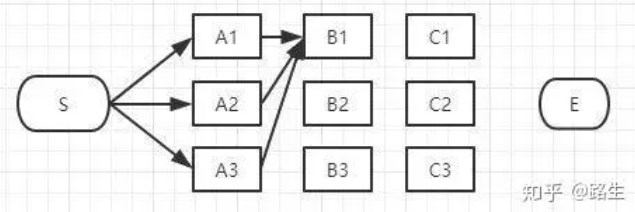

如上图，经过B1的所有路径只有3条：

S-A1-B1

S-A2-B1

S-A3-B1
如果说最终的第二层的节点是从B1经过的话，肯定要从这三条路径中选择一条最短的路径，那么其他的两条可以删除了。
<2>然后我们开始了第二层的第二个节点：

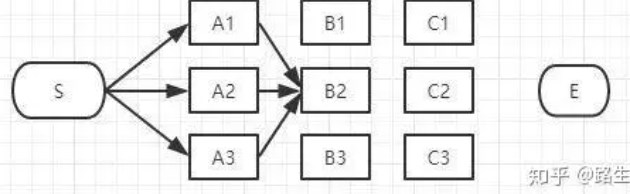
同理，如上图，经过B2的路径有3条：

S-A1-B2

S-A2-B2

S-A3-B2
如果说最终的第二层的节点是从B2经过的话，肯定要从这三条路径中选择一条最短的路径，那么其他的两条可以删除了。

<3>然后我们开始了第二层的第三个个节点：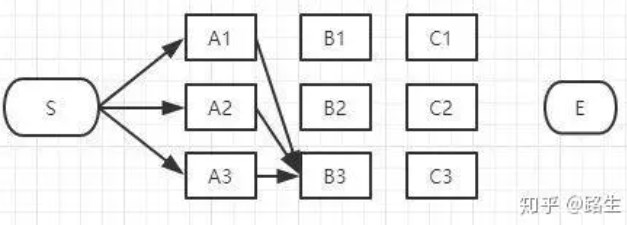

同理，如上图，经过B3的路径也有3条：

S-A1-B3

S-A2-B3

S-A3-B3
如果说最终的第二层的节点是从B3经过的话，肯定要从这三条路径中选择一条最短的路径，那么其他的两条可以删除了。
<4>所有第二层的阶段遍历完了之后，剩下三条路径了。

我们还没有足够的信息判断哪一条一定是全局最短路径的子路径。
(3)然后我们在第三层继续这个算法:
下来讲到C列了，类似上面说的B列，我们从C1、C2、C3一个个节点分析。
经过C1节点的路径有：

S-A3-B1-C1、

S-A1-B2-C1、

S-A2-B3-C1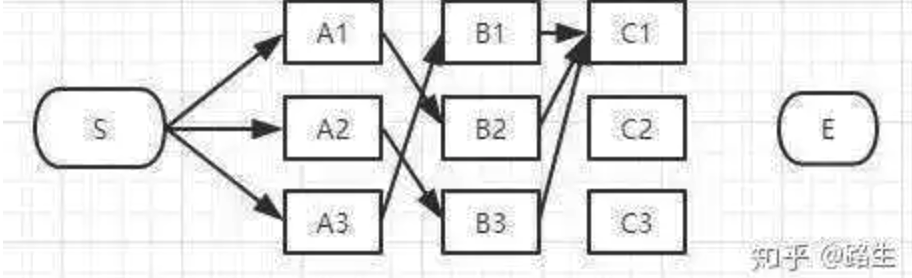

和B列的做法一样，从这三条路径中找到最短的那条（假定是S-A3-B1-C1），其它两条路径同样道理可以删掉了。那么经过C1的所有路径只剩一条，如下图：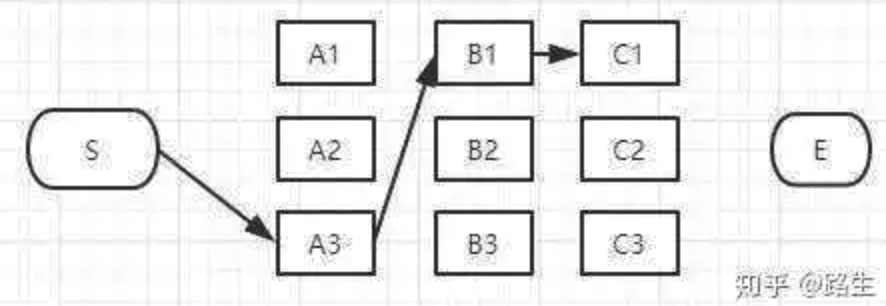

同理，我们可以找到经过C2和C3节点的最短路径，汇总一下：

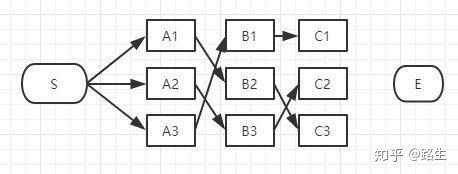
我们还没有足够的信息判断哪一条一定是全局最短路径的子路径。
(4)然后我们在最后一层继续这个算法: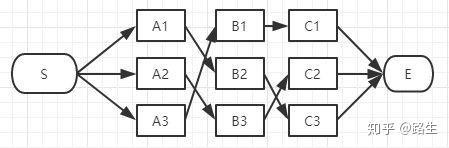

E点已经是终点了，我们稍微对比一下这三条路径的总长度就能知道哪条是最短路径了。

参考文章
https://clyyuanzi.gitbooks.io/julymlnotes/content/hmm.html
http://www.52nlp.cn/category/hidden-markov-model
https://www.lookfor404.com/%E7%94%A8%E9%9A%90%E9%A9%AC%E5%B0%94%E5%8F%AF%E5%A4%AB%E6%A8%A1%E5%9E%8Bhmm%E5%81%9A%E5%91%BD%E5%90%8D%E5%AE%9E%E4%BD%93%E8%AF%86%E5%88%AB-ner%E7%B3%BB%E5%88%97%E4%BA%8C/
https://www.zhihu.com/question/35866596/answer/236886066
http://www.hankcs.com/ml/conditional-random-field.html

https://www.zhihu.com/question/20136144/answer/763021768

对于CRF，直接用最大熵准则建模p(Y|X)的概率。
而HMM，是在做了markov假设下去建模p(Y,X)（即一切观察量的联合概率分布）

多模型评估的指标可以分为以下几个类别

一.Accuracy，Precision，Recall

要计算这几个指标先要了解几个概念：
FN：False Negative,被判定为负样本，但事实上是正样本。
FP：False Positive,被判定为正样本，但事实上是负样本。
TN：True Negative,被判定为负样本，事实上也是负样本。
TP：True Positive,被判定为正样本，事实上也是证样本。
1.Accuracy (准确率)
$ac=\frac {TP+TN}{TP+TN+FP+FN}$

2.Precision(精确率、查准率)
$P = \frac {TP}{TP+FP}$
解释：正样本占分类器所分的正样本的比例

3.Recall(召回率，查全率)
$R = \frac {TP}{TP + FN}$
解释：正样本占真正的正样本的比例

二、现实模型中的准招率

1.正样本的准确率，召回率

我们平常所说的准确率，召回率通常指正样本的，因为我们模板大多比较关心正样本。
$P = \frac {TP}{TP+FP}$
$R = \frac {TP}{TP + FN}$

2.负样本的准确率，召回率

$P = \frac {TN}{TN+FN}$
$R = \frac {TN}{TN + FP}$

3.整个样本的准确率，召回率

这里就要考虑宏平均和微平均

宏平均（Macro-averaging）

是先对每一个类统计指标值，然后在对所有类求算术平均值。

微平均（Micro-averaging）

是对数据集中的每一个实例不分类别进行统计建立全局混淆矩阵，然后计算相应指标。

三、F1值

F1值是精确率和召回率的调和均值，即F1=2PR/(P+R)，相当于精确率和召回率的综合评价指标。

四、PR曲线

五、ROC曲线

1.定义

ROC全称是“受试者工作特征”(Receiver OperatingCharacteristic)曲线。我们根据学习器的预测结果，把阈值从0变到最大，即刚开始是把每个样本作为正例进行预测，随着阈值的增大，学习器预测正样例数越来越少，直到最后没有一个样本是正样例。在这一过程中，每次计算出两个重要量的值，分别以它们为横、纵坐标作图，就得到了“ROC曲线”。
###### 2.横纵坐标轴
纵坐标：真阳率：$TPR = \frac {TP}{TP + FN}$
横坐标：假阳率(误判率)：$FPR = \frac {TP}{TN + FP}$

3.为什么ROC曲线比PR曲线稳定

1.如果正负样本比例差不多，roc曲线和pr曲线基本一致。
2.如果样本比例失调，roc曲线比pr曲线更能判定模型好坏。
3.举个极端的例子：
100个去医院看病，其中99个艾滋病，一个正常人，结果医生将100个人都看成艾滋病人。则：
TP=99
FP=1
TN=0
FN=0
则：P=99%,R =100%,则PR曲线的效果就很好，实际分类效果不好
而：ROC曲线：TPR=100% ，FPR=100%，可看出ROC曲线效果不好，与实际一直。可以看出ROC曲线更好

六、AUC值

1.定义

那么这个指标代表什么呢？这个指标想表达的含义，简单来说其实就是随机抽出一对样本（一个正样本，一个负样本），然后用训练得到的分类器来对这两个样本进行预测，预测得到正样本的概率大于负样本概率的概率。

2.计算

• (1) 1. 最直观的
  根据AUC这个名称，我们知道，计算出ROC曲线下面的面积，就是AUC的值。事实上，这也是在早期 Machine Learning文献中常见的AUC计算方法。由于我们的测试样本是有限的。我们得到的AUC曲线必然是一个阶梯状的。因此，计算的AUC也就是这些阶梯 下面的面积之和。这样，我们先把score排序(假设score越大，此样本属于正类的概率越大)，然后一边扫描就可以得到我们想要的AUC。但是，这么 做有个缺点，就是当多个测试样本的score相等的时候，我们调整一下阈值，得到的不是曲线一个阶梯往上或者往右的延展，而是斜着向上形成一个梯形。此 时，我们就需要计算这个梯形的面积。由此，我们可以看到，用这种方法计算AUC实际上是比较麻烦的。
• (2)AUC的很有趣的性质
  它和Wilcoxon-Mann-Witney Test是等价的。而Wilcoxon-Mann-Witney Test就是测试任意给一个正类样本和一个负类样本，正类样本的score有多大的概率大于负类样本的score。

在有M个正样本,N个负样本的数据集里。一共有MN对样本（一对样本即，一个正样本与一个负样本）。统计这MN对样本里，正样本的预测概率大于负样本的预测概率的个数。

，其中，

这样说可能有点抽象，我举一个例子便能够明白。

假设有4条样本。2个正样本，2个负样本，那么M*N=4。即总共有4个样本对。分别是：
（D,B）,（D,A）,(C,B),（C,A）。
在（D,B）样本对中，正样本D预测的概率大于负样本B预测的概率（也就是D的得分比B高），记为1
同理，对于（C,B）。正样本C预测的概率小于负样本C预测的概率，记为0.
最后可以算得，总共有3个符合正样本得分高于负样本得分，故最后的AUC为

在这个案例里，没有出现得分一致的情况，假如出现得分一致的时候，例如：

同样本是4个样本对，对于样本对（C,B）其I值为0.5。

最后的AUC为

一、背景

自从transformer出来之后，后面的算法基本上都是基于这个为基础，比如bert是以Encode层，GPT系列的GPT、GPT2、GPT3都是Decode层，下面我们主要讲解一下GPT-2。

1、论文

论文名字：《Language Models are Unsupervised Multitask Learners》
论文地址：Language Models are Unsupervised Multitask Learners

2、论文发表时间

时间：2019年2月
团队：openAI、特斯拉老板马斯克的公司

3、源码

源码：https://github.com/openai/gpt-2
官网：https://www.openai.com/blog/better-language-models/

二、架构

1、架构图

:注意：
GPT 使用 Transformer 的 Decoder 结构，并对 Transformer Decoder 进行了一些改动，原本的 Decoder 包含了两个 Multi-Head Attention 结构，GPT 只保留了 Mask Multi-Head Attention

2、网络结构参数

因为GPT-2在刚开始的时候openAI并没有开源，而是分了四个阶段放出来，每次放出来的预训练模型参数也不一样。
网络层数：24层
参数个数：15亿
参数文件大小：
训练数据大小：40G
最大上下文字数：1024

三、GPT-2相对于GPT的改进

GPT-2依然沿用GPT单向transformer的模式，只不过做了一些改进与改变。那GPT-2相对于GPT有哪些不同呢？看看下面几方面：

1. 增加数据集：

既然要博览群书，当然得先有书，所以GPT-2收集了更加广泛、数量更多的语料组成数据集。该数据集包含800万个网页，大小为40G。当然这些数据集是过滤后得到的高质量文本，这样效果才能更好的哦~

2. 增加网络参数：

GPT-2将Transformer堆叠的层数增加到48层，隐层的维度为1600，参数量更是达到了15亿。15亿什么概念呢，Bert的参数量也才只有3亿哦~当然，这样的参数量也不是说谁都能达到的，这也得取决于money的多少啊~

3. GPT-2去掉了fine-tuning层：

不再针对不同任务分别进行微调建模，而是不定义这个模型应该做什么任务，模型会自动识别出来需要做什么任务。这就好比一个人博览群书，你问他什么类型的问题，他都可以顺手拈来，GPT-2就是这样一个博览群书的模型。

4. 调整transformer：

将layer normalization放到每个sub-block之前，并在最后一个Self-attention后再增加一个layer normalization。

5. 其他：

GPT-2将词汇表数量增加到50257个；最大的上下文大小 (context size) 从GPT的512提升到了1024 tokens；batchsize增加到512。

6.Byte-level字节对编码

四、删除finue-tune直接做下游任务

1、Reading Comprehension：

使用 CoQA 数据集。输入是 document + conversation history + A: 来引导出答案。

2、Summarization：

用 TL;DR: 引导出摘要。

3、Translation：

为了引导模型做翻译，先找一个英法句子对 (en1, fr1)，然后想翻译英语句子 en 的时候，输入是 en1 = fr1 + en =，期待模型自己通过类比知道人类是想让他做翻译。结果模型真的悟出了一点儿道，fr-en 的翻译结果是 11.5 BLEU。这一结果是令人震惊的，因为模型在预训练的时候就没见过法语。用一个 byte-level language detector(https://github.com/CLD2Owners/cld2) 做更详细的分析发现，预训练的数据里混入了 10 MB 法语语料。考虑到语料的量级很少，这一结果依然是令人震惊的。

4、Natural Questions：

也是一个 QA 任务，为引导模型做问答，先搞一个 example qa pair (q1, a1)，然后给模型输入 q1 + a1 + q，模型就会回答出 q 的答案。