一、100G数据，1G内存如何排序

思路：多路归并排序

L1 L2正则化的区别

一、算法背景

1论文

Yoon Kim在论文(2014 EMNLP) Convolutional Neural Networks for Sentence Classification提出TextCNN。

将卷积神经网络CNN应用到文本分类任务，利用多个不同size的kernel来提取句子中的关键信息（类似于多窗口大小的ngram），从而能够更好地捕捉局部相关性。

二、算法过程

TextCNN主要过程分为四部，也可以说是四个层。

• Embedding(文本向量化)：将文本中的每个词语转换成相同维度的词向量。
• Convolution(卷积层)：通过不同卷积核的大小kernel_size = (1,2,3,4,5)做卷积运算。
• MaxPooling(池化层)：
• FullConnection and Softmax(全连接层)：全连接的 softmax 层，输出每个类别的概率。

整个算法过程论文中所画流程图如下：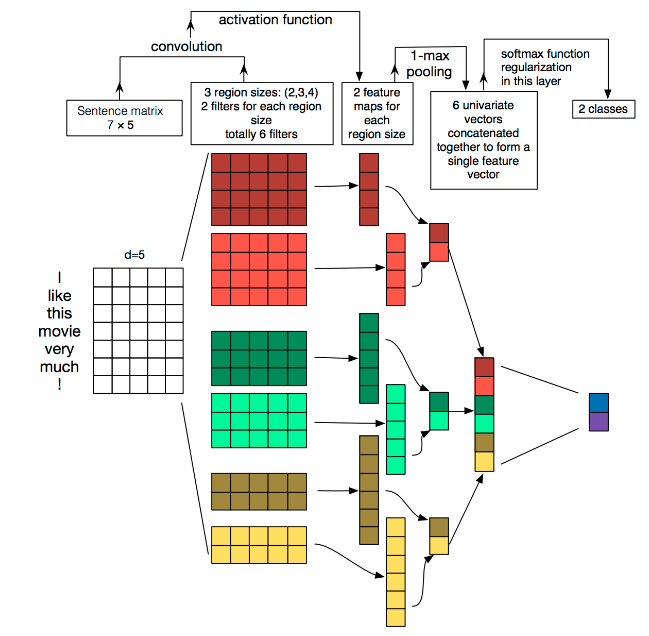

三、算法详解

1.Embedding层

2.Convolution(卷积层)

2.1卷积核的定义
卷积核为一个向量，所以有宽度，和高度。另外卷积核还有一个数量。
2.2:卷积核的宽度
大家在图像处理中经常看到的卷积核都是正方形的，比如44，然后在整张image上沿宽和高逐步移动进行卷积操作。但是nlp中输入的“image”是一个词矩阵，比如n个words，每个word用200维的vector表示的话，这个”image”就是n200的矩阵，卷积核只在高度上已经滑动，在宽度上和word vector的维度一致（=200），也就是说每次窗口滑动过的位置都是完整的单词，不会将几个单词的一部分“vector”进行卷积，这也保证了word作为语言中最小粒度的合理性。参见上图中第二列方格，卷积核的宽度和词向量的宽度同为d=5
2.3卷积核的高度
可以成为卷积核的大小。通常取值为2,3,4,5等。可以认为是滑动窗口的大小，每次移动窗口可以卡2个字或者3个字，4个字，类似n-gram模型。参见上图中第二列方格，卷积核的高度为2,3,4
2.4卷积核的数量
比如卷积核大小为2的可以有100个数量。参见上图中第二列方格，卷积核的数量都是2个
2.5卷积的计算
例如：
1 1 0
0 0 1
1 1 1
1 0 1
0 0 0
与卷积核
1 1 1
0 1 1
计算 结果为
3
3
4
2
计算结果shape=（sentence_len - filter_size + 1, 1）
参见上图第三列，如果卷积核数量为2，则会计算出来两个shape=（sentence_len - filter_size + 1, 1）的向量。
如果是图像的卷积计算参考图片：
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-2DBLArZv-1600566815219)(https://raw.githubusercontent.com/listwebit/ImgDate/master/cnn-2.gif)]

3.MaxPooling(池化层)

池化层的作用：保留显著特征、降低特征维度

池化/采样的方式通常有以下两种：
1、Max-Pooling: 选择Pooling窗口中的最大值作为采样值；
2、Mean-Pooling: 将Pooling窗口中的所有值相加取平均，以平均值作为采样值

3.1最大池化
(1)如果卷积核的数量都是2，则会在两个向量中每个向量里面找个最大值，组成一个新向量。
(2)将所有向量拼接
例如上图

4.FullConnection and Softmax(全连接层)

- 阅读剩余部分 -

一、CRF模型的基本元素

1、 CRF的五个基本元素

HMM中，有5个基本元素：{I,O,A,B,π}，我结合序列标志任务对这5个基本元素做一个介绍：

(1)I:状态序列。在这里，是指每一个词语背后的标注。
(2)O:观测序列。在这里，是指每一个词语本身。
(3)A:转移特征函数(状态转移概率矩阵)：$m_kt_k(y_{i-1},y_i,x,i)$,k为特征个数
(4)B:状态特征函数(观测概率矩阵)：$u_ls_l(y_i,x,i)$,$l$为特征个数

2、CRF模型

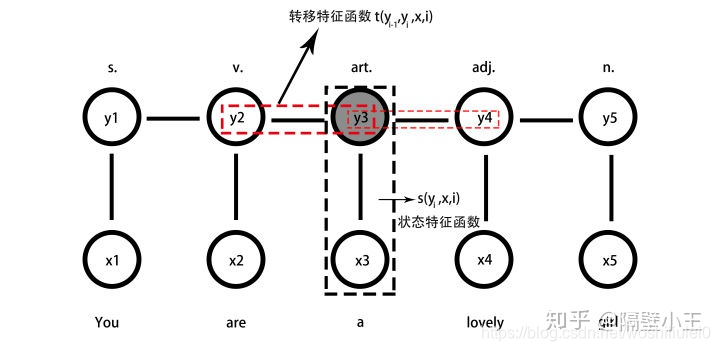
建模函数：
$P(y|x)=\frac{1}{Z(x)} exp(\sum λ_kt_k(y_{i-1},y_i,x,i)+\sum u_ls_l(y_i,x,i))$

3、CRF模型的一个假设

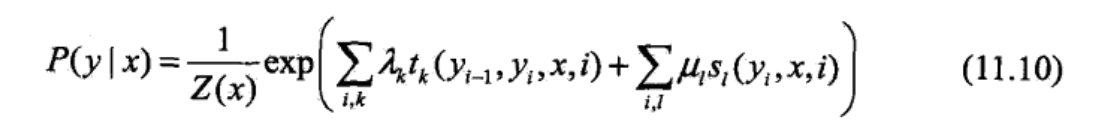
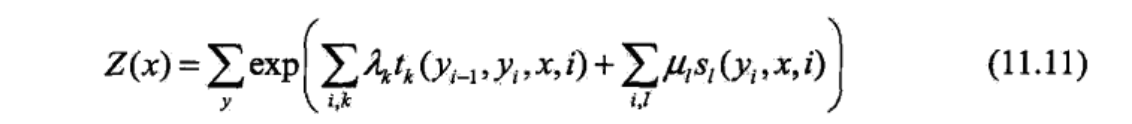
假设：满足马尔科夫性：
$P(Y_i|X,Y_1,....,Y_{i-1},Y_{i+1},...y_n)=P(Y_i|X,Y_{i-1},Y_{i+1})$

二、CRF模型有三种应用场景

我们做命名实体识别只用到其中的一种——求观察序列的背后最可能的标注序列。CRF解决的三个问题：

1、Evaluation(概率计算问题)

已知模型参数 λ= (A, B, π),计算某个观测序列发生的概率，即求P(O|λ)

2、Learning(学习问题)

给定观测序列$O=(o_1,o_2,...,o_n)$，如何调整模型参数 λ=(π, A, B), 使得P(O|λ)最大？，这个就是求模型的算法

3、Decoding(预测问题或者叫解码问题) 最常用

给定观测序列O和模型 λ，求最有可能的状态序列S(s1,s2,...st+1)。
例如：通过实体标注和训练，我们可以得到模型λ，现在给定了一个观测序列=我在凤凰金融工作，求最有可能的命名实体有哪些，想找到对应的状态序列S=(我，在，凤凰金融，工作)。

三、模型由来

1.HMM假设缺点

• (1)齐次马尔科夫假设（又叫一阶马尔科夫假设）
  隐藏的马尔科夫链在任意时刻t的状态只依赖于前一时刻的状态，与其他时刻状态及观测状态无关。

$P(i_t|i_{t-1},o_{t-1},...,i_1) = P(i_t|i_{t-1})$

• (2)观测独立假设
  任意时刻的观测状态只依赖于该时刻的马尔科夫链的状态，与其他时刻的观测状态无关。

2.CRF优点

因为HMM有两个前提假设，所以HMM注定是局部最优解，无法达到全局最优解，也就无法达到最好的效果。

3.CRF算法

CRF解决了HMM两个假设的缺点，使用概率无向图，提出了两个特征函数
1.定义在边上的转移特征函数：$m_kt_k(y_{i-1},y_i,x,i)$
2.定义在节点上的状态特征函数：$u_ls_l(y_i,x,i)$
每个特征函数前面有系数
注意：

• 1.每个时刻t=i有多个特征函数，每个特征函数取值为1或者0，然后每个序列有多个时刻，所以模型上有两个加。
• 2.每个特征函数其实是个局部特征，可以对局部特征求和，将局部特征转化为全局特征。那么为啥求和是全局特征？其实求和的本意是求乘积，因为e为底的指数和就是乘积的形式，这就需要概率无向图求联合概率分布的算法。
• 3.CRF本质上是求概率无向图的联合概率分布，就是去各个时刻标注同时标注正确的联合概率，那么如何求概率无向图的联合概率分布呢？一般是将联合概率写成若干个子联合概率相乘的形式。也就是将联合概率因子分解。
• 4.联合概率因子分解：概率无向图的联合概率分布表示为其最大团上的随机变量函数的乘积，我们平时所说的CRF指的是线性连CRF，所以说每个时刻的i,o构成了一个最大团，所以证明了全局最优解就是局部最优解的和的形式。

参考：
1.https://spaces.ac.cn/archives/5542/comment-page-1
2.https://www.zhihu.com/question/35866596/answer/236886066
3.https://www.cnblogs.com/pinking/p/9194865.html