2020年9月
XLNet算法详解
一、背景
自从Bert打开两阶段模式的魔法盒开关后,在这条路上,会有越来越多的同行者,Bert系列的算法层出不穷,比较注明的有RoBerta,ALBert。Bert系列的算法都属于AutoEncode LM。与之相对应的还要AutoRegressive LM。
1.自回归语言模型(Autoregressive LM)
- 定义
在ELMO/BERT出来之前,大家通常讲的语言模型其实是根据上文内容预测下一个可能跟随的单词,就是常说的自左向右的语言模型任务,或者反过来也行,就是根据下文预测前面的单词,这种类型的LM被称为自回归语言模型。GPT 就是典型的自回归语言模型。ELMO尽管看上去利用了上文,也利用了下文,但是本质上仍然是自回归LM,这个跟模型具体怎么实现有关系。ELMO是做了两个方向(从左到右以及从右到左两个方向的语言模型),但是是分别有两个方向的自回归LM,然后把LSTM的两个方向的隐节点状态拼接到一起,来体现双向语言模型这个事情的。所以其实是两个自回归语言模型的拼接,本质上仍然是自回归语言模型。
- 优缺点
自回归语言模型有优点有缺点,
(1)缺点:是只能利用上文或者下文的信息,不能同时利用上文和下文的信息,当然,貌似ELMO这种双向都做,然后拼接看上去能够解决这个问题,因为融合模式过于简单,所以效果其实并不是太好。
(2)优点:其实跟下游NLP任务有关,比如生成类NLP任务,比如文本摘要,机器翻译等,在实际生成内容的时候,就是从左向右的,自回归语言模型天然匹配这个过程。而Bert这种DAE模式,在生成类NLP任务中,就面临训练过程和应用过程不一致的问题,导致生成类的NLP任务到目前为止都做不太好。
2.自编码语言模型(Autoencoder LM)
- 定义
自回归语言模型只能根据上文预测下一个单词,或者反过来,只能根据下文预测前面一个单词。相比而言,Bert通过在输入X中随机Mask掉一部分单词,然后预训练过程的主要任务之一是根据上下文单词来预测这些被Mask掉的单词,如果你对Denoising Autoencoder比较熟悉的话,会看出,这确实是典型的DAE的思路。那些被Mask掉的单词就是在输入侧加入的所谓噪音。类似Bert这种预训练模式,被称为DAE LM。
- 优缺点
(1)优点:这种DAE LM的优缺点正好和自回归LM反过来,它能比较自然地融入双向语言模型,同时看到被预测单词的上文和下文,这是好处。
(2)缺点:是啥呢?主要在输入侧引入[Mask]标记,导致预训练阶段和Fine-tuning阶段不一致的问题,因为Fine-tuning阶段是看不到[Mask]标记的。DAE吗,就要引入噪音,[Mask] 标记就是引入噪音的手段,这个正常。
3.引入xlnet
XLNet的出发点就是:能否融合自回归LM和DAE LM两者的优点。就是说如果站在自回归LM的角度,如何引入和双向语言模型等价的效果;如果站在DAE LM的角度看,它本身是融入双向语言模型的,如何抛掉表面的那个[Mask]标记,让预训练和Fine-tuning保持一致。当然,XLNet还讲到了一个Bert被Mask单词之间相互独立的问题,我相信这个不太重要,原因后面会说。当然,我认为这点不重要的事情,纯粹是个人观点,出错难免,看看就完了,不用较真。
二、XLNet
1.排列语言模型
那么,怎么能够在单词Ti的上文中Contenxt_before中揉入下文Context_after的内容呢?你可以想想。XLNet是这么做的,在预训练阶段,引入Permutation Language Model的训练目标。什么意思呢?就是说,比如包含单词Ti的当前输入的句子X,由顺序的几个单词构成,比如x1,x2,x3,x4四个单词顺序构成。我们假设,其中,要预测的单词Ti是x3,位置在Position 3,要想让它能够在上文Context_before中,也就是Position 1或者Position 2的位置看到Position 4的单词x4。可以这么做:假设我们固定住x3所在位置,就是它仍然在Position 3,之后随机排列组合句子中的4个单词,在随机排列组合后的各种可能里,再选择一部分作为模型预训练的输入X。比如随机排列组合后,抽取出x4,x2,x3,x1这一个排列组合作为模型的输入X。于是,x3就能同时看到上文x2,以及下文x4的内容了。这就是XLNet的基本思想,所以说,看了这个就可以理解上面讲的它的初衷了吧:看上去仍然是个自回归的从左到右的语言模型,但是其实通过对句子中单词排列组合,把一部分Ti下文的单词排到Ti的上文位置中,于是,就看到了上文和下文,但是形式上看上去仍然是从左到右在预测后一个单词。
但是要注意的是:在预训练的时候并不是先对语料进行排序,这个排序操作是在Attention过程中通过mask来实现的,预训练语料的输入还是按照正常的顺利x1,x2,x3,x4来输入的。(为什么不能用乱序的语料呢?因为在微调期间你的语料不可能是乱序的,使用的话,你的预训练和微调就出现不一致问题了)就算用了排列语言模型,为什么标准的语言模型就不行了呢?
论文里面有解释:
首先我们要知道的是,标准的语言模型使用的标准的Attention操作,那么为什么标准的Attention会失效呢?
怎么理解呢:
我们标准的语言模型(Attention)都是预测的下一个字,并不会带上要预测字的位置信息,比如,x1,x2,x3,x4,如果我们要预测t=3也就是x3的时候,我们是根据x1,x2的信息(内容和位置)去预测,并不会带上x3的位置信息。但是排列语言模型不在适应了,排列:x1,x2,x3,x4和x1,x2,x4,x3,那么如还用标准的attention,这两种排列模型预测的t=3时刻的字就没有区别了,实际情况是不一样的,因为我们输入的序列是x1,x2,x3,x4,但是在attention mask之后这两种排列是不一样的。
排列:x1,x2,x3,x4在预测t=3时刻,预测的x1,x2,__,__ 是第三个位置。
排列:x1,x2,x4,x3在预测t=3时刻,预测的x1,x2,__,__ 是第四个位置。
为了解决这个问题,xlnet提出了双流注意力机制。
2.双流自注意力机制(Two-Stream Self-Attention )
- 内容流:content stream
使用: ,内容流失一个标准的Attention,对上下文和Xzt本身编码,例如要预测t时刻的内容,content用的是t之前的(不包括t)的上下文,和t时刻的内容。
,内容流失一个标准的Attention,对上下文和Xzt本身编码,例如要预测t时刻的内容,content用的是t之前的(不包括t)的上下文,和t时刻的内容。
注意:content stream虽然包含本身单词的意思,但是预测的时候我们并不是根据content去预测的。而是用query流去预测的。- 查询流:query stream
使用: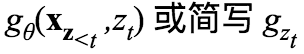 ,查询流是一个mask自己的attention,对上下文和Xzt时刻的位置编码,例如要预测t时刻的内容,query用的是t之前的(不包括t)的上下文,和t时刻的位置。
,查询流是一个mask自己的attention,对上下文和Xzt时刻的位置编码,例如要预测t时刻的内容,query用的是t之前的(不包括t)的上下文,和t时刻的位置。
注意:query stream不包含本身单词的意思,但是预测的时候是根据query去预测的。而query流的计算要用到content流。具体例子可以参考图片:
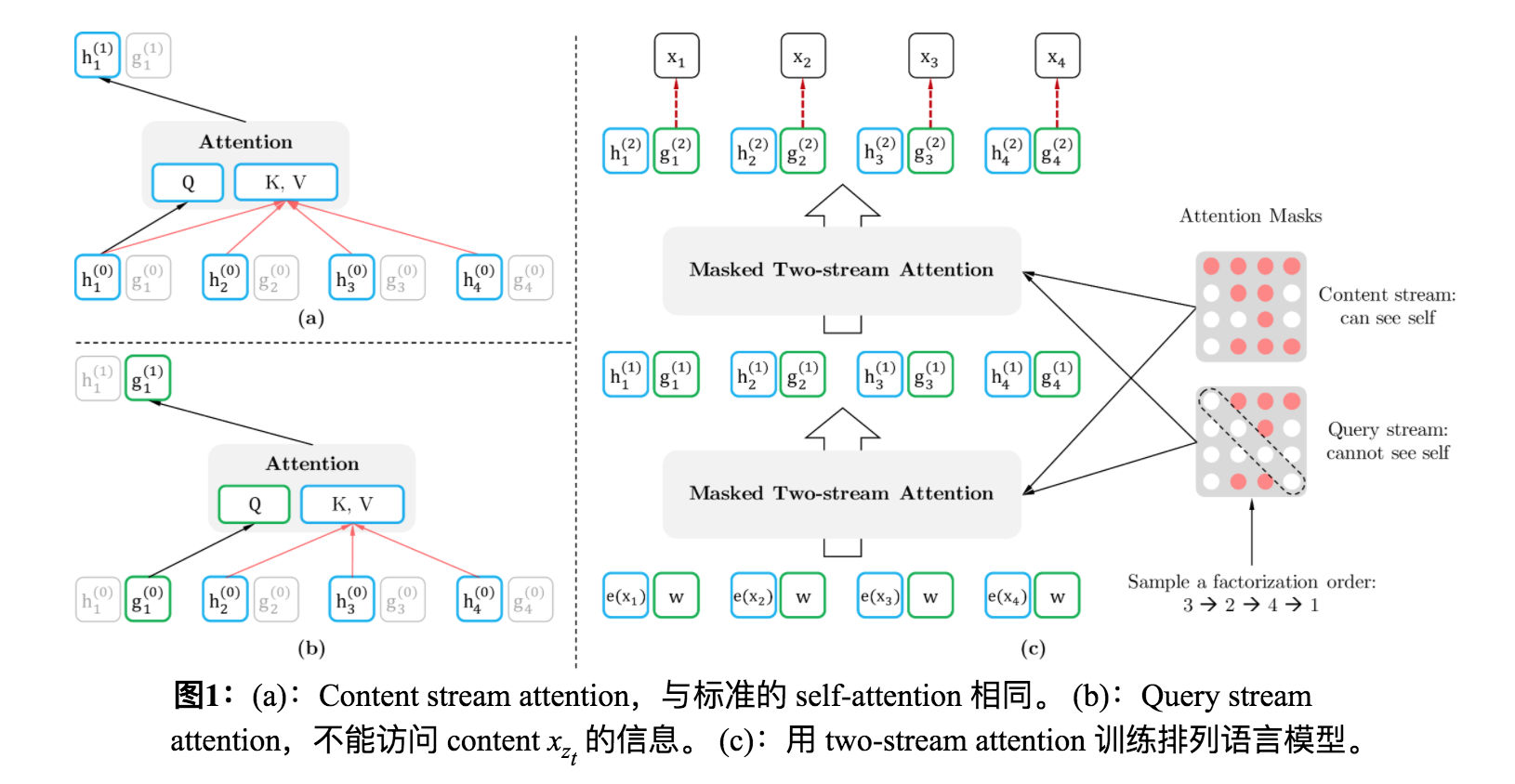
在pretrain阶段,在输出端对查询流向量预测相应的token,如上图中最后一个公式。在finetune阶段,只需要内容流向量,不再需要查询流向量。3.NSP去掉
4.使用transformer-xl
5.Partial Prediction(部分预测)

参考文献:
1.https://arxiv.org/pdf/1906.08237.pdf
2.https://yiyibooks.cn/nlp/XLNet/index.html
roberta算法详解
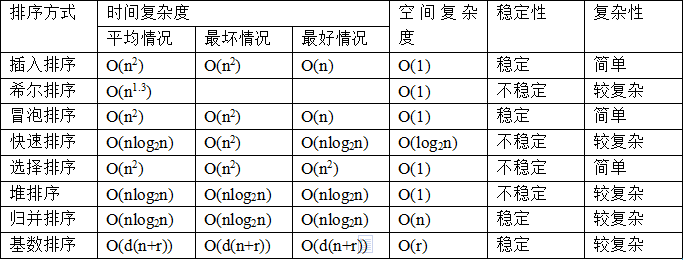
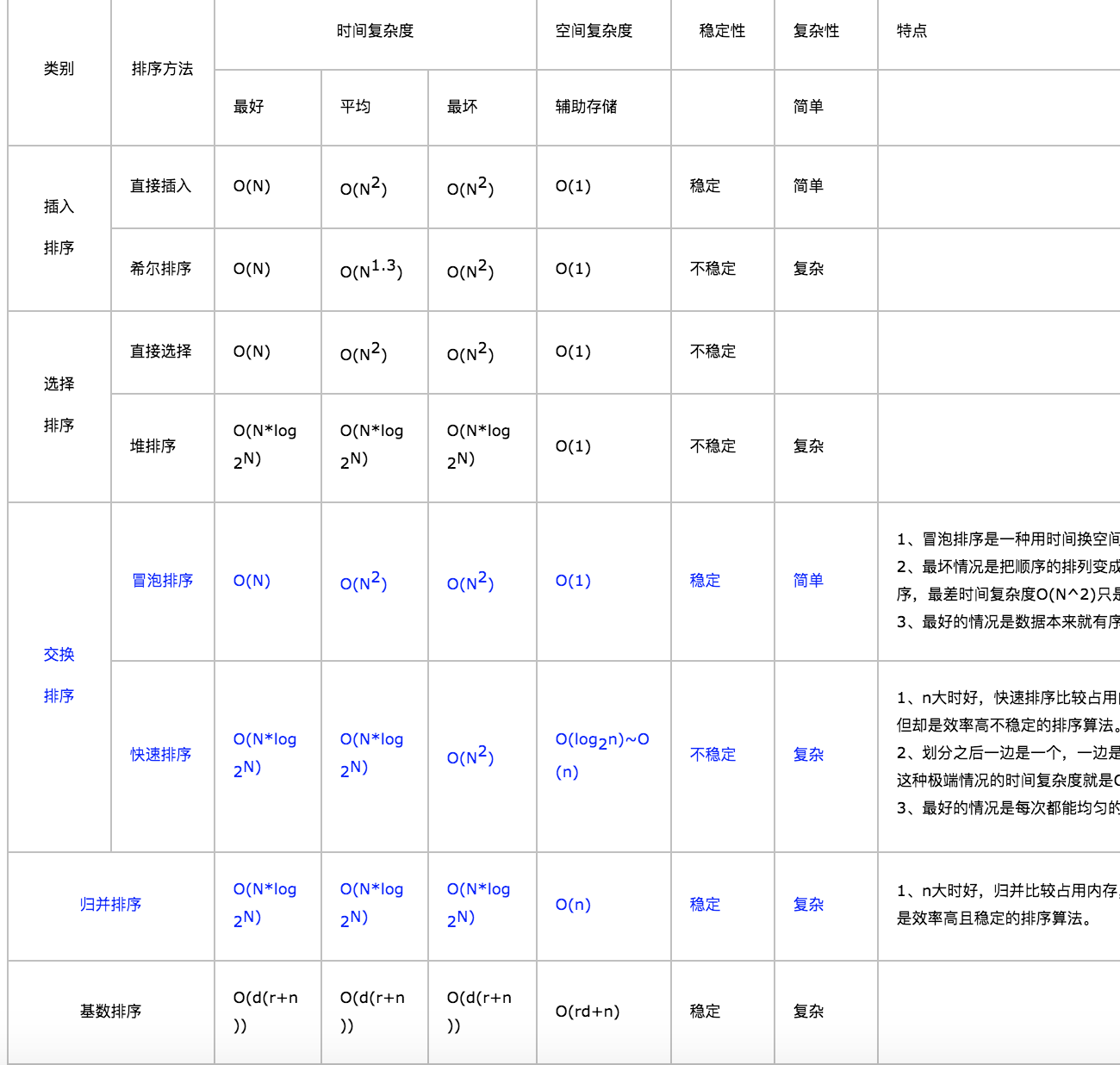
八大排序算法
分类方式
一.交换排序:1.冒泡排序,2.快速排序
二.插入排序:3.直接插入排序,4.希尔排序
三.选择排序:5.简单选择排序,6.堆排序
四.7.归并排序
五.8.基数排序
python实现
一、冒泡排序
思路:
两层循环:
第一层代表最右边最大数的位置。
第二层用来对比交换找出剩下的最大数
def sort(arr):
l = len(arr)
# 遍历所有数组元素
for i in range(l):
for j in range(0, l-i-1):
if arr[j] > arr[j+1] :
arr[j], arr[j+1] = arr[j+1], arr[j]
arr = [64, 34, 25, 12, 22, 11, 90]
sort(arr)
print (arr)
二、快速排序
1.递归排序算法
思路:
2.非递归排序算法
思路:和递归比较像,用栈来存划分区间,
在先找一个锚点,一最右边为例,通过锚点来划分子区间
参考:https://zhuanlan.zhihu.com/p/60756341
# -*- coding: UTF-8 -*-
# 递归排序算法
def sort(b):
"""快速排序"""
if len(b) < 2:
return b
# 选取基准,随便选哪个都可以,选中间的便于理解
mid = b[len(b)// 2]
# 定义基准值左右两个数列
left, right = [], []
# 从原始数组中移除基准值
b.remove(mid)
for item in b:
# 大于基准值放右边
if item >= mid:
right.append(item)
else:
# 小于基准值放左边
left.append(item)
# 使用迭代进行比较
return sort(left) + [mid] + sort(right)
#非递归排序算法
def quicksortUnRecur( nums, beg, end):
if beg >= end:
return nums
stack = [beg, end]
while stack:
beg, end = stack.pop(0), stack.pop(0)
if beg >= end:
continue
i, pivot = beg-1, nums[end]
for j in range(beg, end+1):
if nums[j] <= pivot:
i += 1
nums[i], nums[j] = nums[j], nums[i]
stack.extend([beg, i-1, i+1, end])
b = [11, 99, 33, 69, 77, 88, 55, 11, 33, 36, 39, 66, 44, 22]
print sort(b)三、直接插入排序
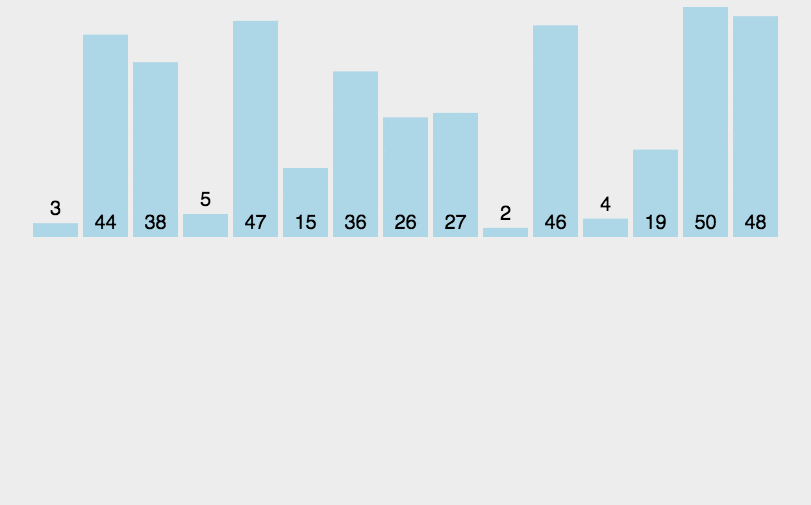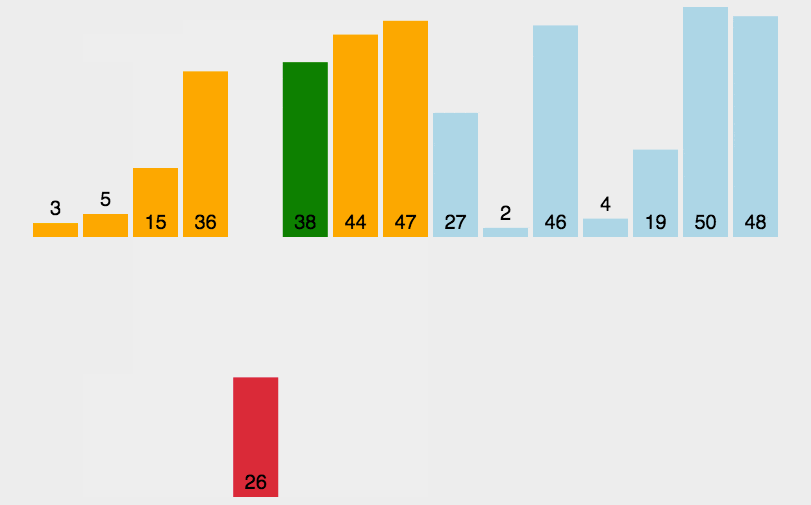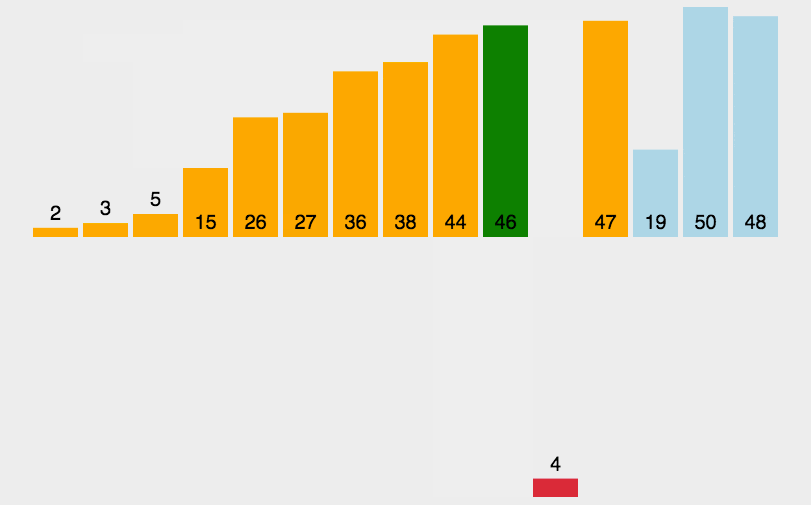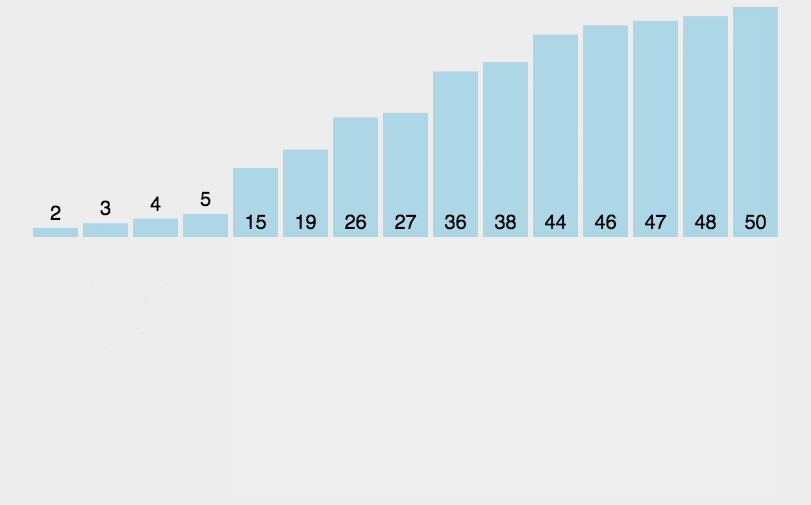
1.思路
它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。
2.两种写法
有两种写法但是本质是一样的:
(1)标准的:不交换
- 设置一层循环,可以从0,也可以从1,都一样
- 然后设一个变量key=arr[i],key用来记录,不交换,让后加while
(2)参考冒泡排序:交换
- 设置一层循环,可以从0,也可以从1,都一样
- 在设置一层循环,注意使用倒叙range(i-1, -1, -1),然后进行交换
(1)标准的:不交换
# -*- coding: UTF-8 -*-
def sort(arr):
l = len(arr)
for i in range(1, l):
key = arr[i]
j = i-1
while j >=0 and key < arr[j] :
arr[j+1] = arr[j]
j -= 1
arr[j+1] = key
arr = [12, 11, 13, 5, 6]
sort(arr)
print(arr)(2)参考冒泡排序:交换
# -*- coding: UTF-8 -*-
def insert(arr):
l = len(arr)
for i in range(l):
for j in range(i-1, -1, -1):
if arr[j] > arr[j+1]:
arr[j+1], arr[j] = arr[j], arr[j+1]
else:
break
arr = [9, 5, 6, 7, 8 ]
insert(arr)
print arr四、希尔排序
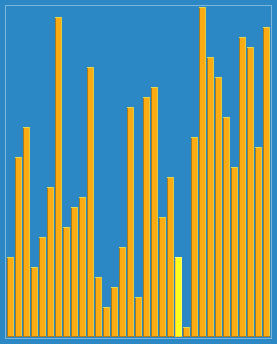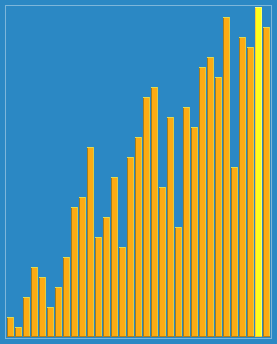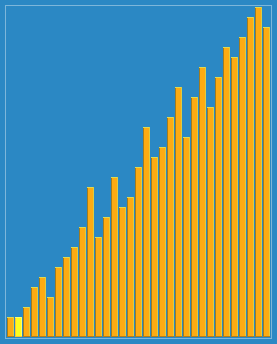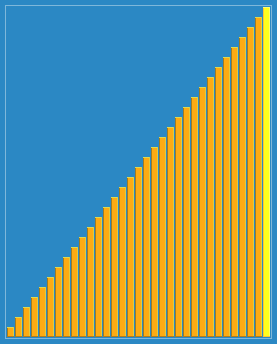
1.思路
希尔排序,也称递减增量排序算法,是插入排序的一种更高效的改进版本。但希尔排序是非稳定排序算法
# -*- coding: UTF-8 -*-
def shellSort(arr):
n = len(arr)
gap = int(n / 2)
while gap > 0:
for i in range(gap, n):
temp = arr[i]
j = i
while j >= gap and arr[j - gap] > temp:
arr[j] = arr[j - gap]
j -= gap
arr[j] = temp
gap = int(gap / 2)
arr = [12, 34, 54, 2, 3]
shellSort(arr)
print arr
五、简单选择排序
1.思路
选择排序(Selection sort)是一种简单直观的排序算法。它的工作原理如下。首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置,然后,再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。
# -*- coding: UTF-8 -*-
def selectsort(arr):
l = len(arr)
for i in range(l):
min_idx = i
for j in range(i + 1, l):
if arr[min_idx] > arr[j]:
min_idx = j
arr[i], arr[min_idx] = arr[min_idx], arr[i]
arr = [64, 25, 12, 22, 11]
selectsort(arr)
print (arr)六、堆排序
1.思路
# -*- coding: UTF-8 -*-
def heapify(arr, n, i):
largest = i
l = 2 * i + 1 # left = 2*i + 1
r = 2 * i + 2 # right = 2*i + 2
if l < n and arr[i] < arr[l]:
largest = l
if r < n and arr[largest] < arr[r]:
largest = r
if largest != i:
arr[i],arr[largest] = arr[largest],arr[i] # 交换
heapify(arr, n, largest)
def heapSort(arr):
n = len(arr)
# Build a maxheap.
for i in range(n, -1, -1):
heapify(arr, n, i)
# 一个个交换元素
for i in range(n-1, 0, -1):
arr[i], arr[0] = arr[0], arr[i] # 交换
heapify(arr, i, 0)
arr = [ 12, 11, 13, 5, 6, 7]
heapSort(arr)
print arr七、归并排序
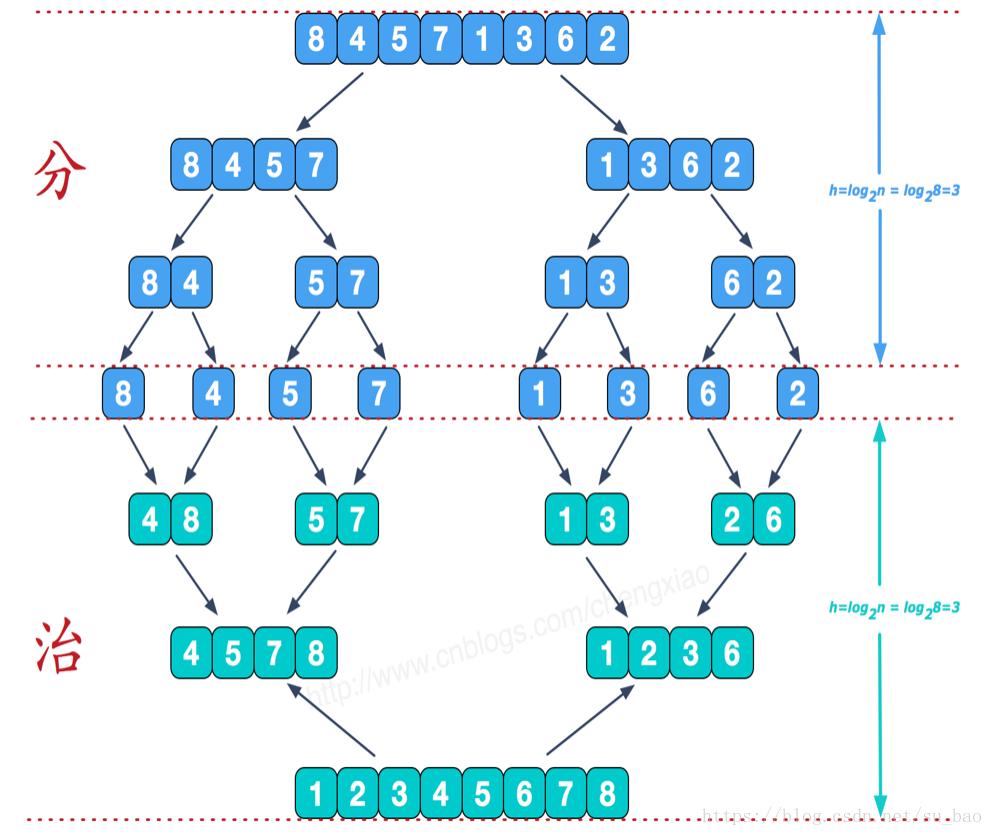
1.思路
归并排序采用分而治之的原理:
一、将一个序列从中间位置分成两个序列;
二、在将这两个子序列按照第一步继续二分下去;
三、直到所有子序列的长度都为1,也就是不可以再二分截止。这时候再两两合并成一个有序序列即可。
# -*- coding: UTF-8 -*-
def merge(a, b):
c = []
h = j = 0
while j < len(a) and h < len(b):
if a[j] < b[h]:
c.append(a[j])
j += 1
else:
c.append(b[h])
h += 1
if j == len(a):
for i in b[h:]:
c.append(i)
else:
for i in a[j:]:
c.append(i)
return c
def merge_sort(lists):
if len(lists) <= 1:
return lists
middle = len(lists)/2
left = merge_sort(lists[:middle])
right = merge_sort(lists[middle:])
return merge(left, right)
if __name__ == '__main__':
a = [4, 7, 8, 3, 5, 9]
print merge_sort(a)
八、基数排序
1.思路
# -*- coding: UTF-8 -*-

七大查找
分类方法
一、二分查找
二、
一、二分查找
1.思路
要求必须是有序列表
2.两种写法
1.递归查找
2.非递归查找
1.递归查找
# -*- coding: UTF-8 -*-
def binary_search1(arr, left, right, num):
if left > right: #递归结束条件
return -1
mid = (left + right) // 2
if num < arr[mid]:
right = mid -1
elif num > arr[mid]:
left = mid + 1
else:
return mid
return binary_search(arr, left, right, num)
#这里之所以会有return是因为必须要接收值,不然返回None
#回溯到最后一层的时候,如果没有return,那么将会返回None
arr = [11, 32, 51, 21, 42, 9, 5, 6, 7, 8]
print(arr)
arr.sort()
print(arr)
res = binary_search1(arr, 0, len(arr)-1,9)
print(res)
2.非递归查找
# -*- coding: UTF-8 -*-
def binary_search(arr, num):
left = 0
right = len(lis) - 1
while left <= right: #循环条件
mid = (left + right) // 2 #获取中间位置,数字的索引(序列前提是有序的)
if num < arr[mid]: #如果查询数字比中间数字小,那就去二分后的左边找,
right = mid - 1 #来到左边后,需要将右变的边界换为mid-1
elif num > arr[mid]: #如果查询数字比中间数字大,那么去二分后的右边找
left = mid + 1 #来到右边后,需要将左边的边界换为mid+1
else:
return mid #如果查询数字刚好为中间值,返回该值得索引
return -1 #如果循环结束,左边大于了右边,代表没有找到
arr = [11, 32, 51, 21, 42, 9, 5, 6, 7, 8]
print(arr)
lis.sort()
print(arr)
res = binary_search(arr, 9)
print res